Solve: 6x^2 + 5 = 17x
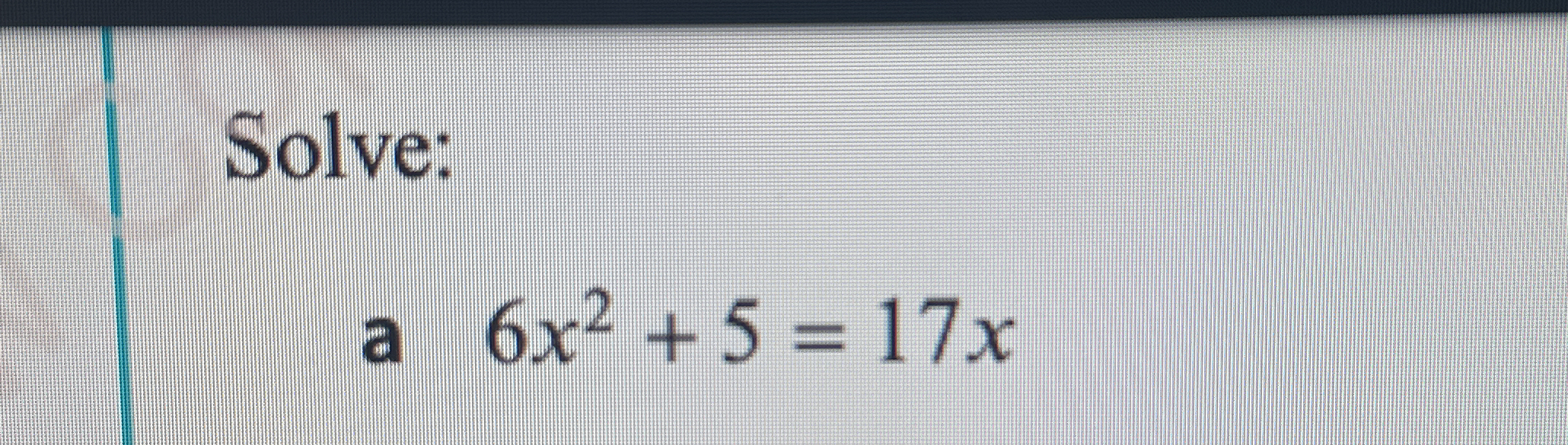
Understand the Problem
The question requires solving the quadratic equation 6x^2 + 5 = 17x for x. This involves rearranging the equation into standard quadratic form (ax^2 + bx + c = 0) and then solving for x using factoring, completing the square, or the quadratic formula.
Answer
$x = \frac{1}{3}, \frac{5}{2}$
Answer for screen readers
$x = \frac{1}{3}, \frac{5}{2}$
Steps to Solve
-
Rearrange the equation Subtract $17x$ from both sides of the equation to set it equal to zero. This puts the equation in the standard quadratic form $ax^2 + bx + c = 0$. $$6x^2 + 5 - 17x = 17x - 17x$$ $$6x^2 - 17x + 5 = 0$$
-
Factor the quadratic equation We need to find two numbers that multiply to $6 \cdot 5 = 30$ and add up to $-17$. These numbers are $-15$ and $-2$. Rewrite the middle term using these numbers: $$6x^2 - 15x - 2x + 5 = 0$$
-
Factor by grouping Factor out the greatest common factor from the first two terms and the last two terms: $$3x(2x - 5) - 1(2x - 5) = 0$$ Now factor out the common binomial factor $(2x - 5)$: $$(3x - 1)(2x - 5) = 0$$
-
Solve for $x$ Set each factor equal to zero and solve for $x$: $$3x - 1 = 0 \Rightarrow 3x = 1 \Rightarrow x = \frac{1}{3}$$ $$2x - 5 = 0 \Rightarrow 2x = 5 \Rightarrow x = \frac{5}{2}$$
$x = \frac{1}{3}, \frac{5}{2}$
More Information
The solutions to a quadratic equation are also called roots or zeros of the quadratic equation.
Tips
A common mistake is incorrectly factoring the quadratic equation. Always double-check your factoring by expanding the factored form to ensure it matches the original quadratic equation. Another mistake is only finding one solution; remember that quadratic equations usually have two solutions.
AI-generated content may contain errors. Please verify critical information