Evaluate the following limit: lim (x->-1) (2x^2 + 5x + 3) / (x + 1)

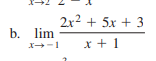
Understand the Problem

The question asks how to evaluate the limit of a rational function as x approaches -1. We will attempt to factor the numerator to see if we can cancel out the (x+1) term in the denominator.

Answer

1

Steps to Solve

Factor the numerator

We need to factor the quadratic expression $2x^2 + 5x + 3$. We are looking for two numbers that multiply to $2 \cdot 3 = 6$ and add up to $5$. These numbers are $2$ and $3$. So we can write $5x$ as $2x + 3x$.

$2x^2 + 5x + 3 = 2x^2 + 2x + 3x + 3$

Now, factor by grouping:

$2x^2 + 2x + 3x + 3 = 2x(x+1) + 3(x+1) = (2x+3)(x+1)$

Simplify the rational function

Substitute the factored form of the numerator into the limit:

$\lim_{x \to -1} \frac{(2x+3)(x+1)}{x+1}$

Since $x \neq -1$, we can cancel out the $(x+1)$ term:

$\lim_{x \to -1} (2x+3)$

Evaluate the limit

Now, we can directly substitute $x = -1$ into the simplified expression:

$2(-1) + 3 = -2 + 3 = 1$

More Information

The limit of the given rational function as $x$ approaches $-1$ is $1$.

Tips

A common mistake is to try to substitute $x = -1$ directly into the original expression, which would result in an indeterminate form $\frac{0}{0}$. It is important to factor and simplify the expression first. Also, errors in factoring the quadratic expression can occur.

AI-generated content may contain errors. Please verify critical information

Thank you for voting!