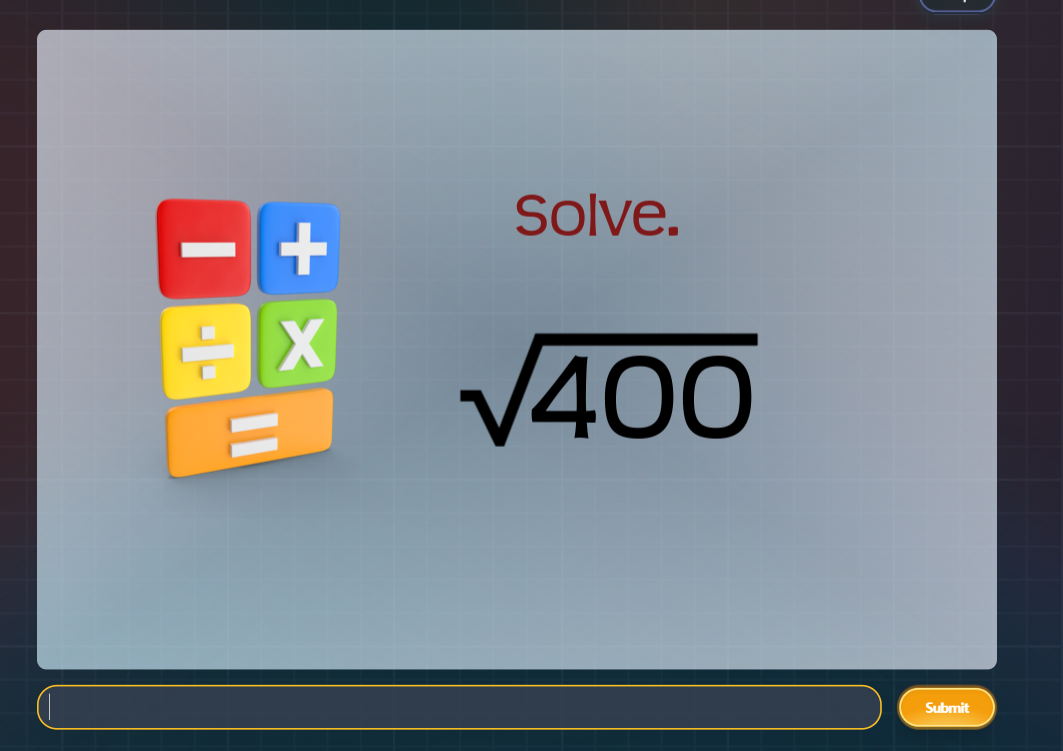
Solve √400.

Understand the Problem

The question is asking to solve the square root of 400. This involves identifying what number, when multiplied by itself, equals 400.

Answer

The square root of $400$ is $20$.

Steps to Solve

Identify the Problem

We're trying to find the square root of 400, written as $\sqrt{400}$.

Determine the Factors of 400

To find the square root, we need to identify what number multiplied by itself equals 400. The factors of 400 are:

$1 \times 400$
$2 \times 200$
$4 \times 100$
$5 \times 80$
$8 \times 50$
$10 \times 40$
$16 \times 25$
$20 \times 20$

Locate the Pairing

The pair that multiplies to give us 400 with equal factors is $20 \times 20$. This indicates that the square root of 400 is 20.

Write the Final Expression

Thus, we can express the solution as:

$$ \sqrt{400} = 20 $$

The final answer is $20$.

More Information

The square root of a number is a value that, when multiplied by itself, will give the original number. The square root of 400 is commonly encountered in various mathematical applications, especially in geometry, where it might represent the side length of a square with an area of 400 square units.

Tips

Confusing the concept of squaring and taking square roots. Remember that squaring a number means multiplying it by itself, while taking a square root is finding what number produces a given value when squared.
Forgetting to consider that some numbers have two square roots, one positive and one negative. In this case, while $20$ is the principal square root, $-20$ is also valid.

AI-generated content may contain errors. Please verify critical information

Thank you for voting!