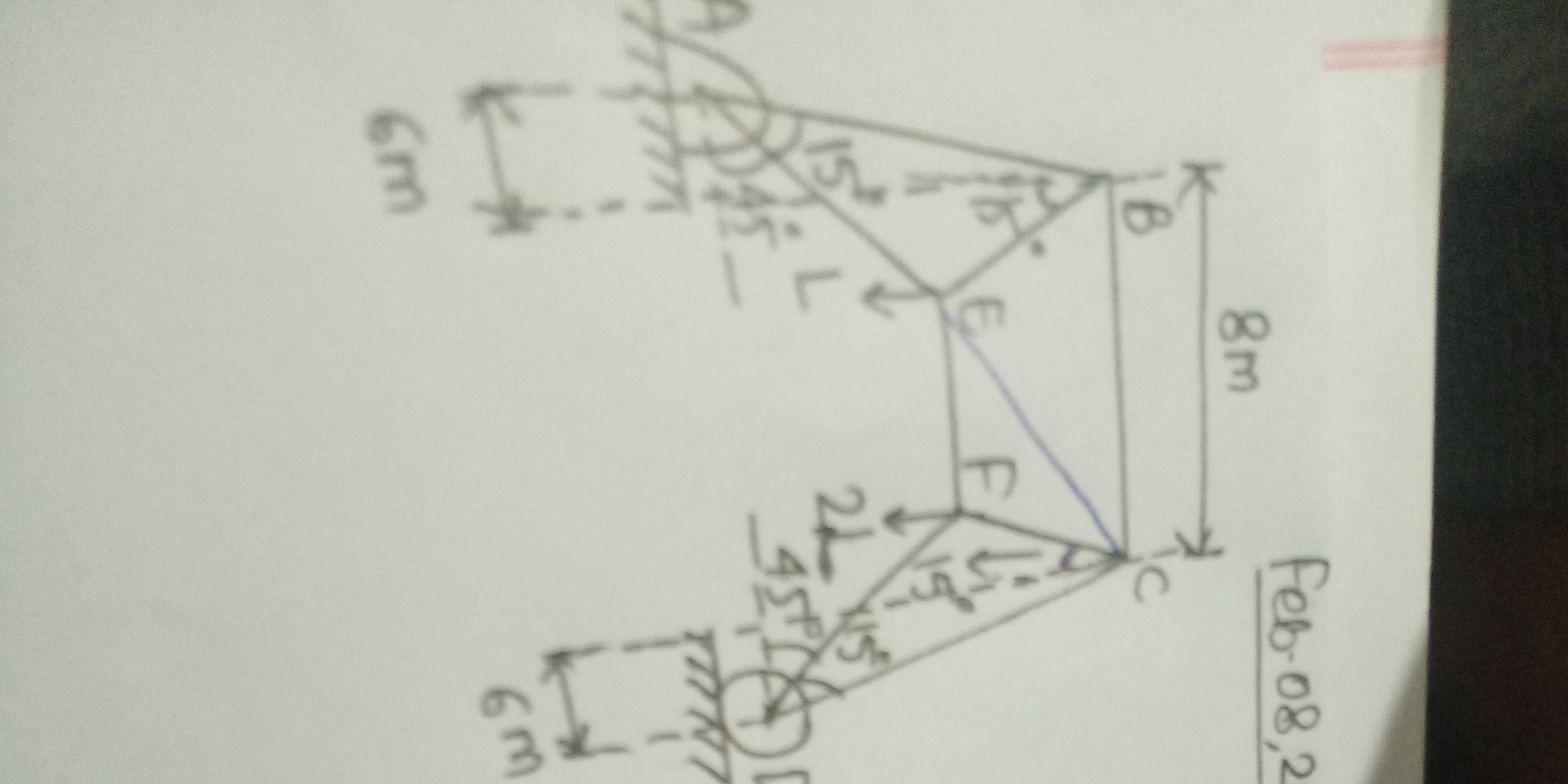
Understand the Problem
The question appears to involve a geometric problem with angles and lengths, likely requiring calculations based on the provided diagram.
Answer
The angle \( \theta \) can be calculated as \( \theta = \tan^{-1}\left(\frac{8}{3}\right) \), leading to segment length calculations via right triangles.
Answer for screen readers
The lengths and angles will depend on the specific triangle calculations, but using the formulas, we can determine various segments. For instance, if ( \theta ) is approximately ( 69.44^\circ ), we can find side lengths related to ( E ).
Steps to Solve
- Identify Triangle and Angles
From the diagram, we can see two right triangles formed, one above the line segment ( BC ) and one below. Let's denote the angles at point ( E ) and their respective positions.
- Use Trigonometry for Right Triangles
For triangle ( BEC ):
- The height ( BE = 8 ) m and the base ( EC = 3 ) m.
Using the tangent function for angle ( BEC ), $$ \tan(\theta) = \frac{opposite}{adjacent} = \frac{BE}{EC} $$
- Calculate ( \theta )
Setting the values, $$ \tan(\theta) = \frac{8}{3} $$
To find ( \theta ), we calculate: $$ \theta = \tan^{-1}\left(\frac{8}{3}\right) $$
- Determine Length ( EF )
For triangle ( AEF ), using the given angles, we can use the sine or cosine rule as appropriate. The height ( EF ) can be solved by: $$ EF = AE \cdot \sin(\alpha) $$ where ( \alpha ) is known.
- Solve for Total Lengths
Add up the lengths calculated in steps for the complete dimensions.
The lengths and angles will depend on the specific triangle calculations, but using the formulas, we can determine various segments. For instance, if ( \theta ) is approximately ( 69.44^\circ ), we can find side lengths related to ( E ).
More Information
Using trigonometric functions in right triangles helps find unknown lengths and angles effectively, which is applicable in various geometric problems.
Tips
- Misidentifying angles: Ensure angles are from the correct triangles.
- Incorrect use of sine and cosine: Confirm which function to use based on the opposite, adjacent, or hypotenuse.
AI-generated content may contain errors. Please verify critical information