Find the volume of the solid generated by revolving the region bounded by x=0, y=10, y = x+2 around x=10 using cylindrical shell and washer methods.
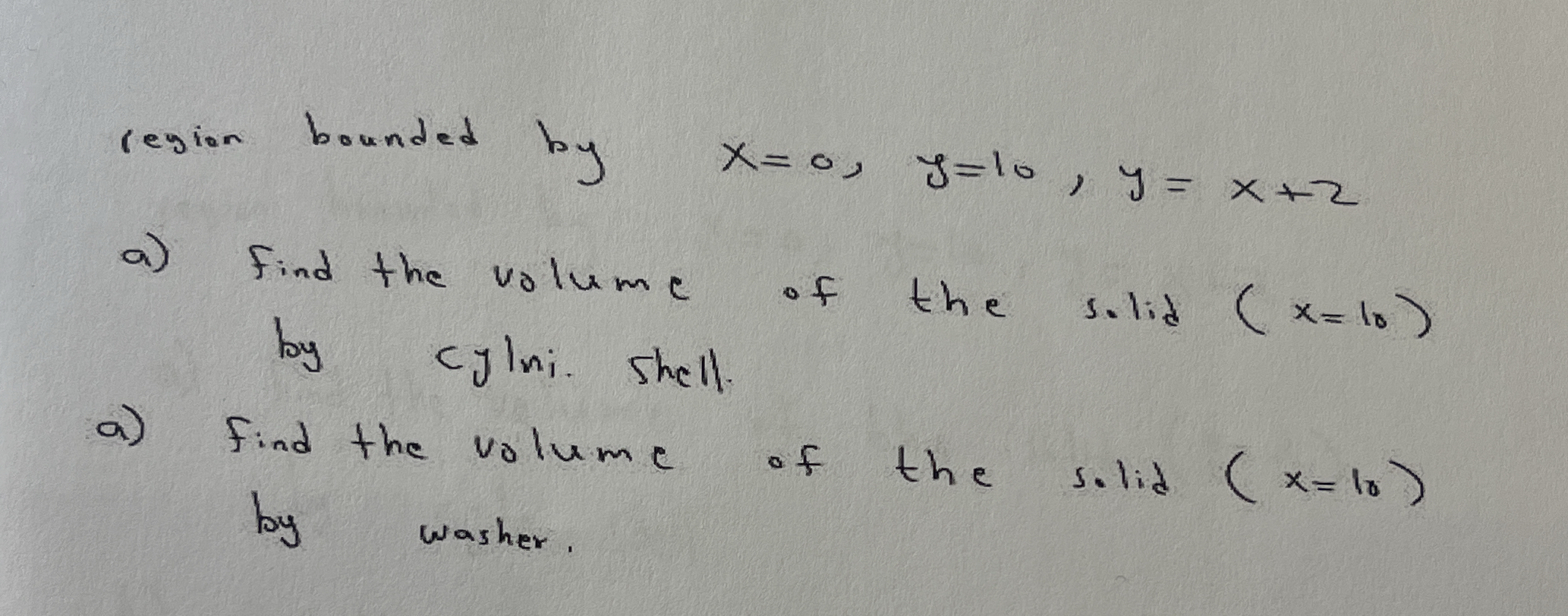
Understand the Problem
The question asks to find the volume of a solid generated by revolving a region bounded by the given equations around the line x=10. The volume must be calculated using both the cylindrical shell method and the washer method.
Answer
$V = \frac{1408\pi}{3}$
Answer for screen readers
$V = \frac{1408\pi}{3}$
Steps to Solve
- Find the intersection points of the given equations
First, find where $y = x + 2$ and $y = 10$ intersect to define the limits of integration. Set the equations equal to each other: $x + 2 = 10$ $x = 8$ So, the intersection point is at $x = 8$. Since we are also bounded by $x=0$, our limits of integration will range from 0 to 8.
- Cylindrical Shell Method Setup
The volume using cylindrical shells around $x = 10$ is given by $$V = 2\pi \int_a^b (10-x)h(x) , dx$$ where $a$ and $b$ are the limits of integration along the x-axis, and $h(x)$ is the height of the shell at a given $x$ value. In this case, $a = 0$, $b = 8$, and $h(x) = 10 - (x + 2) = 8 - x$.
- Cylindrical Shell Method Integration
Now, evaluate the integral: $$V = 2\pi \int_0^8 (10 - x)(8 - x) , dx$$ $$V = 2\pi \int_0^8 (80 - 10x - 8x + x^2) , dx$$ $$V = 2\pi \int_0^8 (x^2 - 18x + 80) , dx$$ $$V = 2\pi \left[ \frac{x^3}{3} - 9x^2 + 80x \right]_0^8$$ $$V = 2\pi \left[ \frac{8^3}{3} - 9(8^2) + 80(8) \right] - 2\pi \left[ 0 \right]$$ $$V = 2\pi \left[ \frac{512}{3} - 576 + 640 \right]$$ $$V = 2\pi \left[ \frac{512}{3} + 64 \right]$$ $$V = 2\pi \left[ \frac{512 + 192}{3} \right]$$ $$V = 2\pi \left[ \frac{704}{3} \right]$$ $$V = \frac{1408\pi}{3}$$
- Washer Method Setup
Using the washer method with respect to $y$, the volume is given by $$V = \pi \int_c^d (R(y)^2 - r(y)^2) , dy$$ where $c$ and $d$ are the limits of integration along the y-axis, $R(y)$ is the outer radius, and $r(y)$ is the inner radius. Here, the limits of integration are $c = 2$ and $d = 10$. The outer radius is $R(y) = 10 - 0 = 10$, and the inner radius is $r(y) = 10 - (y - 2) = 12 - y$.
- Washer Method Integration
Now, evaluate the integral: $$V = \pi \int_2^{10} (10^2 - (12 - y)^2) , dy$$ $$V = \pi \int_2^{10} (100 - (144 - 24y + y^2)) , dy$$ $$V = \pi \int_2^{10} (100 - 144 + 24y - y^2) , dy$$ $$V = \pi \int_2^{10} (-y^2 + 24y - 44) , dy$$ $$V = \pi \left[ -\frac{y^3}{3} + 12y^2 - 44y \right]_2^{10}$$ $$V = \pi \left[ -\frac{10^3}{3} + 12(10^2) - 44(10) \right] - \pi \left[ -\frac{2^3}{3} + 12(2^2) - 44(2) \right]$$ $$V = \pi \left[ -\frac{1000}{3} + 1200 - 440 \right] - \pi \left[ -\frac{8}{3} + 48 - 88 \right]$$ $$V = \pi \left[ -\frac{1000}{3} + 760 \right] - \pi \left[ -\frac{8}{3} - 40 \right]$$ $$V = \pi \left[ -\frac{1000}{3} + 760 + \frac{8}{3} + 40 \right]$$ $$V = \pi \left[ -\frac{992}{3} + 800 \right]$$ $$V = \pi \left[ \frac{-992 + 2400}{3} \right]$$ $$V = \pi \left[ \frac{1408}{3} \right]$$ $$V = \frac{1408\pi}{3}$$
$V = \frac{1408\pi}{3}$
More Information
The volume remains the same whether calculated by the cylindrical shell method or the washer method as it should be.
Tips
A common mistake when using the cylindrical shell method is to incorrectly calculate the radius or height of the cylindrical shells. For example, forgetting to subtract x from 10 to get the correct radius. Similarly, for the washer method, errors in calculating the inner and outer radius or setting up the integration limits are common. Always visualize the region and the axis of rotation to help prevent these mistakes.
AI-generated content may contain errors. Please verify critical information