Simplify the following expression: (-x^2 + 9xy) - (x^2 + 6xy - 8y^2)
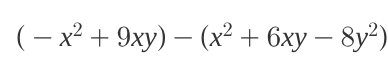
Understand the Problem
The question is asking to simplify the expression by combining like terms after distributing the negative sign. We need to subtract the second polynomial from the first.
Answer
$-2x^2 + 3xy + 8y^2$
Answer for screen readers
$-2x^2 + 3xy + 8y^2$
Steps to Solve
- Distribute the negative sign
Distribute the negative sign to each term inside the second parentheses: $$(-x^2 + 9xy) - (x^2 + 6xy - 8y^2) = -x^2 + 9xy - x^2 - 6xy + 8y^2$$
- Combine like terms
Combine the $x^2$ terms, the $xy$ terms, and the $y^2$ terms: $$(-x^2 - x^2) + (9xy - 6xy) + 8y^2 = -2x^2 + 3xy + 8y^2$$
$-2x^2 + 3xy + 8y^2$
More Information
The simplified expression is a trinomial, which is a polynomial with three terms.
Tips
A common mistake is not distributing the negative sign correctly to all the terms inside the parenthesis. Alternatively, errors can occur when combining the coefficients of like terms (e.g., adding instead of subtracting).
AI-generated content may contain errors. Please verify critical information