Simplify the following expression: \(\frac{3m^{-2}}{2m^{3}}\)
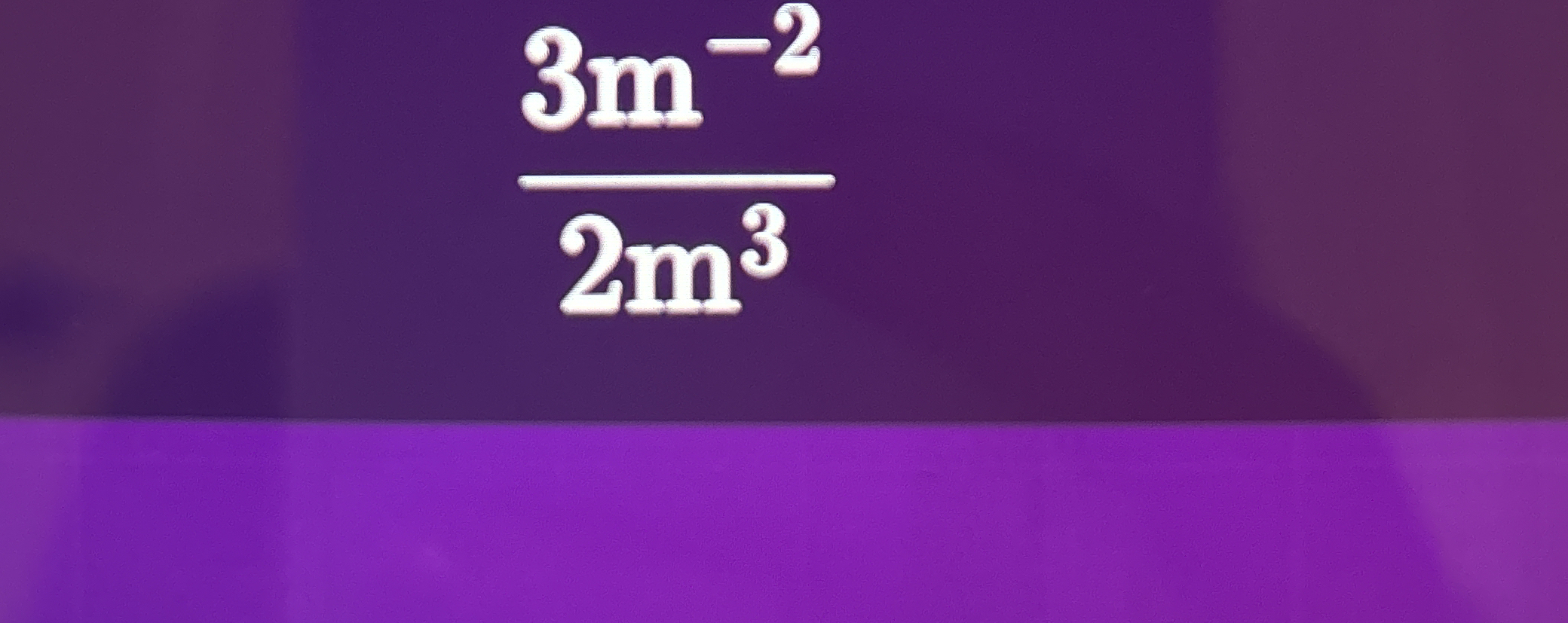
Understand the Problem
The question involves simplifying an algebraic fraction with terms containing exponents. To simplify, we need to apply the rules of exponents, specifically how to handle negative exponents and division of like terms. The overall goal is to simplify the expression to its simplest form.
Answer
$\frac{3}{2m^{5}}$
Answer for screen readers
$\frac{3}{2m^{5}}$
Steps to Solve
-
Rewrite the expression Start with the original expression: $$ \frac{3m^{-2}}{2m^{3}} $$
-
Move the term with the negative exponent Move $m^{-2}$ from the numerator to the denominator to make the exponent positive: $$ \frac{3}{2m^{3}m^{2}} $$
-
Combine like terms in the denominator Use the rule $m^a \cdot m^b = m^{a+b}$ to combine the $m$ terms in the denominator: $$ \frac{3}{2m^{3+2}} = \frac{3}{2m^{5}} $$
$\frac{3}{2m^{5}}$
More Information
The simplified form of the given expression is $\frac{3}{2m^{5}}$. This is achieved by applying the rules of exponents, specifically dealing with negative exponents and combining like terms.
Tips
A common mistake is to incorrectly apply the rules of exponents, especially when dealing with negative exponents. For example, some might mistakenly add the exponents in the original expression instead of moving the term with the negative exponent first. Another mistake could be made where students try to make the coefficient negative somehow.
AI-generated content may contain errors. Please verify critical information