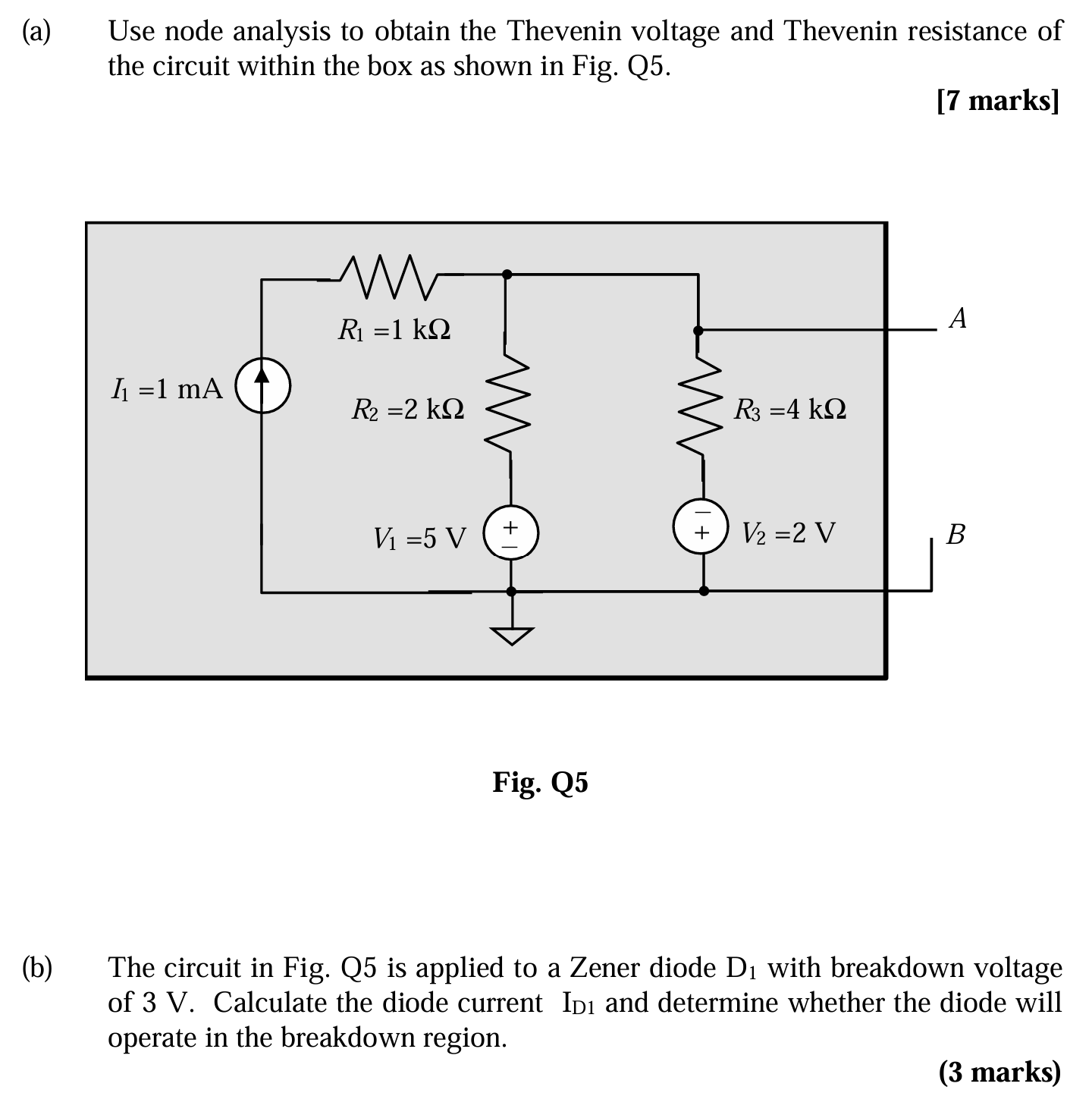
a) Use node analysis to obtain the Thevenin voltage and Thevenin resistance of the circuit within the box as shown in Fig. Q5. b) The circuit in Fig. Q5 is applied to a Zener diode... a) Use node analysis to obtain the Thevenin voltage and Thevenin resistance of the circuit within the box as shown in Fig. Q5. b) The circuit in Fig. Q5 is applied to a Zener diode D₁ with breakdown voltage of 3 V. Calculate the diode current ID1 and determine whether the diode will operate in the breakdown region. Read more

Steps to Solve

1. Find the Thevenin Voltage ($V_{TH}$)

First, we need to determine the Thevenin voltage by finding the open-circuit voltage between terminals A and B. We will use nodal analysis.

Let's define a node voltage $V_A$ at terminal A (relative to ground). Applying Kirchhoff's Current Law (KCL) at node A:

$$ \frac{V_A - V_1}{R_2} + \frac{V_A - V_2}{R_3} + I_1 = 0 $$

Given values: $I_1 = 1 \text{mA} = 0.001 \text{A}$, $R_1 = 1 \text{k}\Omega = 1000 \Omega$, $R_2 = 2 \text{k}\Omega = 2000 \Omega$, $R_3 = 4 \text{k}\Omega = 4000 \Omega$, $V_1 = 5 \text{V}$, $V_2 = 2 \text{V}$

Substituting the values into the equation:

$$ \frac{V_A - 5}{2000} + \frac{V_A - 2}{4000} + 0.001 = 0 $$

Multiplying through by 4000 to clear fractions:

$$ 2(V_A - 5) + (V_A - 2) + 4 = 0 $$

$$ 2V_A - 10 + V_A - 2 + 4 = 0 $$

$$ 3V_A - 8 = 0 $$

$$ 3V_A = 8 $$

$$ V_A = \frac{8}{3} \text{V} $$

Therefore, the Thevenin voltage $V_{TH} = V_A = \frac{8}{3} \text{V} \approx 2.67 \text{V}$.

2. Find the Thevenin Resistance ($R_{TH}$)

To find the Thevenin resistance, we need to deactivate the independent sources. This means replacing the voltage sources with short circuits and the current source with an open circuit. Looking back into the terminals A and B, we see $R_2$ and $R_3$ are in parallel. This parallel combination is then in series with $R_1$, but $R_1$ is shorted by the current source being open. Thus, the Thevenin resistance is just the parallel combination of $R_2$ and $R_3$.

$$ R_{TH} = \frac{R_2 \cdot R_3}{R_2 + R_3} $$

$$ R_{TH} = \frac{2000 \cdot 4000}{2000 + 4000} = \frac{8000000}{6000} = \frac{4000}{3} \Omega $$

Therefore, the Thevenin resistance $R_{TH} = \frac{4000}{3} \Omega \approx 1.33 \text{k}\Omega$.

3. Analyze the Zener Diode Circuit

Now, we connect a Zener diode with a breakdown voltage of 3V to the Thevenin equivalent circuit. The Thevenin equivalent circuit consists of a voltage source $V_{TH}$ in series with a resistor $R_{TH}$.

To determine if the Zener diode is in breakdown, we need to see if the voltage across it would exceed its breakdown voltage if it were not there. Since $V_{TH} = \frac{8}{3} \text{V} \approx 2.67 \text{V}$, which is less than the Zener breakdown voltage of 3V, the diode is NOT in breakdown.

Since the Zener diode is not in breakdown, it acts virtually as an open circuit. Therefore, the current through the diode, $I_{D1} = 0 \text{A}$.