Simplify the following algebraic expressions. (a) 20 ÷ 4b × 5ab (b) (6 × a × a × b) × (-2 × b × a)
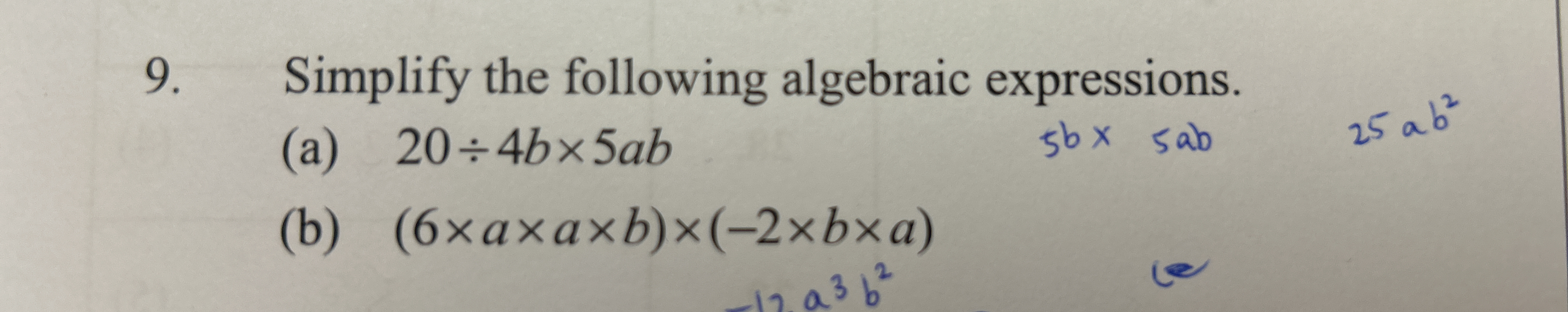
Understand the Problem
The question is asking to simplify two algebraic expressions. The first expression is 20 divided by 4b multiplied by 5ab, and the second is a combination of multiple terms including (6 × a × a × b) multiplied by (-2 × b × a).
Answer
(a) $25a$ (b) $-12a^3b^2$
Answer for screen readers
(a) $25a$
(b) $-12a^3b^2$
Steps to Solve
- Simplifying Expression (a)
Start with the expression ( 20 \div 4b \times 5ab ).
First, divide ( 20 ) by ( 4b ): $$ \frac{20}{4b} = \frac{20 \div 4}{b} = \frac{5}{b} $$
Now, multiply this result by ( 5ab ): $$ \frac{5}{b} \times 5ab = \frac{5 \times 5 \times a \times b}{b} = 25a $$
- Simplifying Expression (b)
Now look at the expression ( (6 \times a \times a \times b) \times (-2 \times b \times a) ).
First, arrange and combine like terms: $$ (6a^2b) \times (-2ab) $$
Now, multiply the coefficients and the variables: $$ 6 \times -2 = -12 $$
For the variables: $$ a^2 \times a \times b \times b = a^{2+1}b^{1+1} = a^3b^2 $$
Putting it all together: $$ -12a^3b^2 $$
(a) $25a$
(b) $-12a^3b^2$
More Information
The simplifications demonstrate basic algebraic principles such as combining like factors, performing multiplication and division involving variables, and applying the rules of exponents.
Tips
- Confusing the order of operations can lead to incorrect simplifications. Always perform division before multiplication unless parentheses indicate otherwise.
- Forgetting to combine like terms or applying exponent rules incorrectly.
AI-generated content may contain errors. Please verify critical information