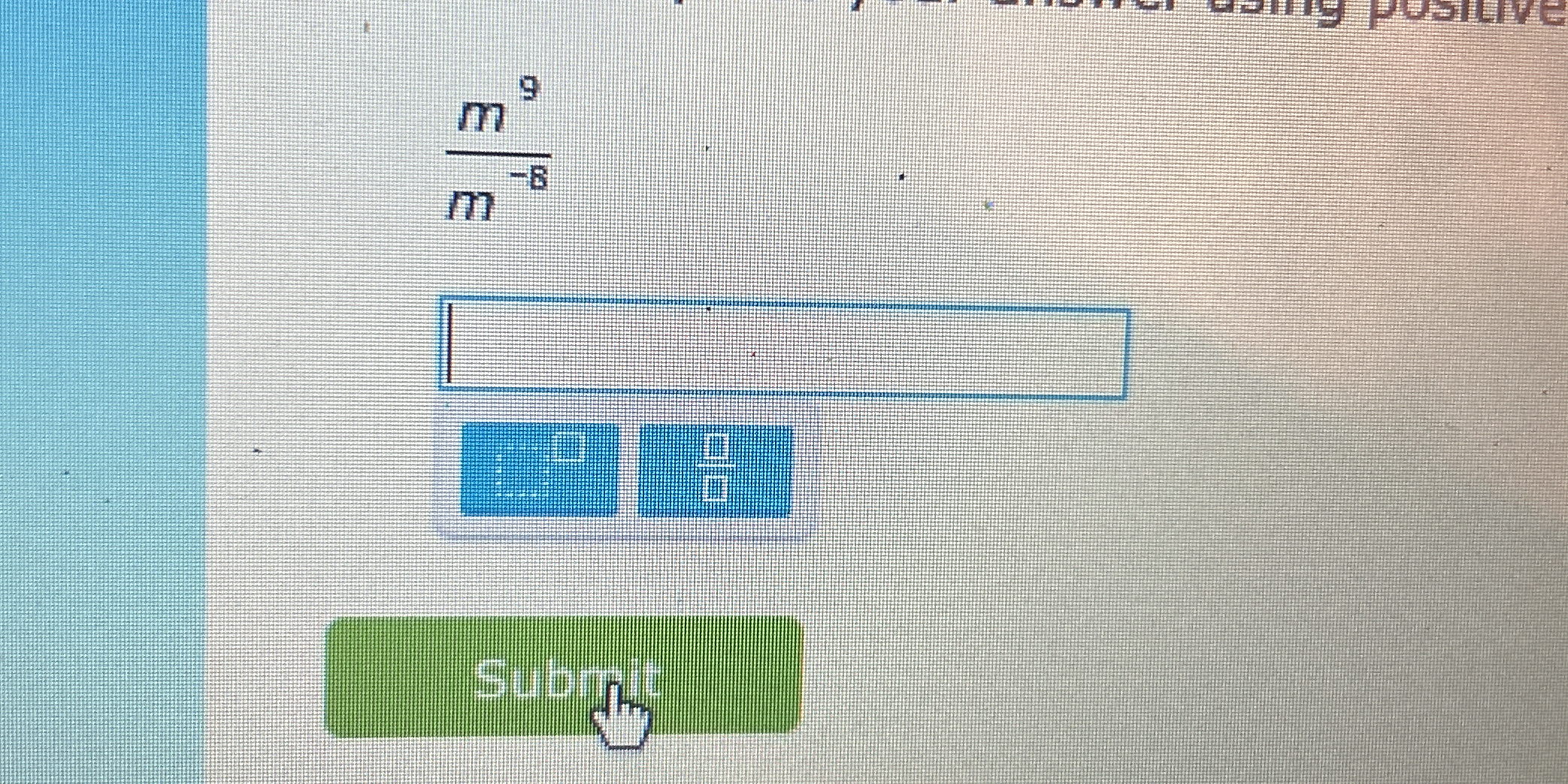
Simplify the expression m^9 / m^-8 using positive exponents.
Understand the Problem
The question involves simplifying the expression ( \frac{m^9}{m^{-8}} ) and providing the answer using positive exponents. This requires applying the laws of exponents.
Answer
The simplified expression is $m^{17}$.
Answer for screen readers
The simplified expression is ( m^{17} ).
Steps to Solve
-
Apply the quotient rule of exponents
When dividing two expressions with the same base, subtract the exponent of the denominator from the exponent of the numerator:
$$ \frac{m^a}{m^b} = m^{a-b} $$ -
Subtract the exponents
In this case, you have ( a = 9 ) and ( b = -8 ). Substitute these values into the equation:
$$ m^{9 - (-8)} $$ -
Simplify the exponent
Subtracting a negative exponent is equivalent to addition:
$$ 9 - (-8) = 9 + 8 = 17 $$
Thus, we have:
$$ m^{17} $$
The simplified expression is ( m^{17} ).
More Information
This result demonstrates how the laws of exponents allow us to manipulate expressions easily. When dividing excerpts, subtracting a negative exponent effectively turns it into an addition, which is key in simplifying calculations.
Tips
- Misinterpreting the negative exponent: Always remember that subtracting a negative is the same as adding.
- Incorrectly applying the exponent rules: Ensure you are familiar with the different rules for multiplying and dividing exponents.
AI-generated content may contain errors. Please verify critical information