Simplify the expression \( \frac{2^{2}y^{-6}}{8^{-1}z^{0}x^{-7}} \)
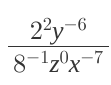
Understand the Problem
The question is presenting a mathematical expression involving variables and exponents, likely asking for simplification or evaluation. To solve it, we will need to apply rules of exponents and possibly simplify the expression as much as possible.
Answer
The simplified expression is \( \frac{32x^7}{y^6} \).
Answer for screen readers
The simplified expression is ( \frac{32x^7}{y^6} ).
Steps to Solve
- Rewrite the base 8 as a power of 2
Since ( 8 = 2^3 ), we can rewrite ( 8^{-1} ) as: $$ 8^{-1} = (2^3)^{-1} = 2^{-3} $$
- Simplify the expression
Now substitute ( 8^{-1} ) into the original expression: $$ \frac{2^2 y^{-6}}{2^{-3} z^0 x^{-7}} $$
- Simplify ( z^0 ) and apply the properties of exponents
Since ( z^0 = 1 ), the expression simplifies to: $$ \frac{2^2 y^{-6}}{2^{-3} \cdot 1 \cdot x^{-7}} = \frac{2^2 y^{-6}}{2^{-3} x^{-7}} $$
- Combine the exponents of ( 2 )
Using the property ( \frac{a^m}{a^n} = a^{m-n} ): $$ 2^{2 - (-3)} = 2^{2 + 3} = 2^5 $$
- Combine the negative exponents
Now, for ( y^{-6} ) over ( x^{-7} ): $$ \frac{y^{-6}}{x^{-7}} = y^{-6} \cdot x^{7} = \frac{x^7}{y^{6}} $$
- Combine everything together
Thus, the final expression is: $$ \frac{2^5 x^7}{y^{6}} $$
The simplified expression is ( \frac{32x^7}{y^6} ).
More Information
The expression simplifies from a complex form containing multiple variables and exponents to a more manageable form. This illustrates the power of applying exponent rules efficiently.
Tips
- Forgetting that ( z^0 = 1 ) and not simplifying it.
- Misapplying the property of exponents when combining ( a^m / a^n ).
- Neglecting to change negative exponents to their positive form during simplification.
AI-generated content may contain errors. Please verify critical information