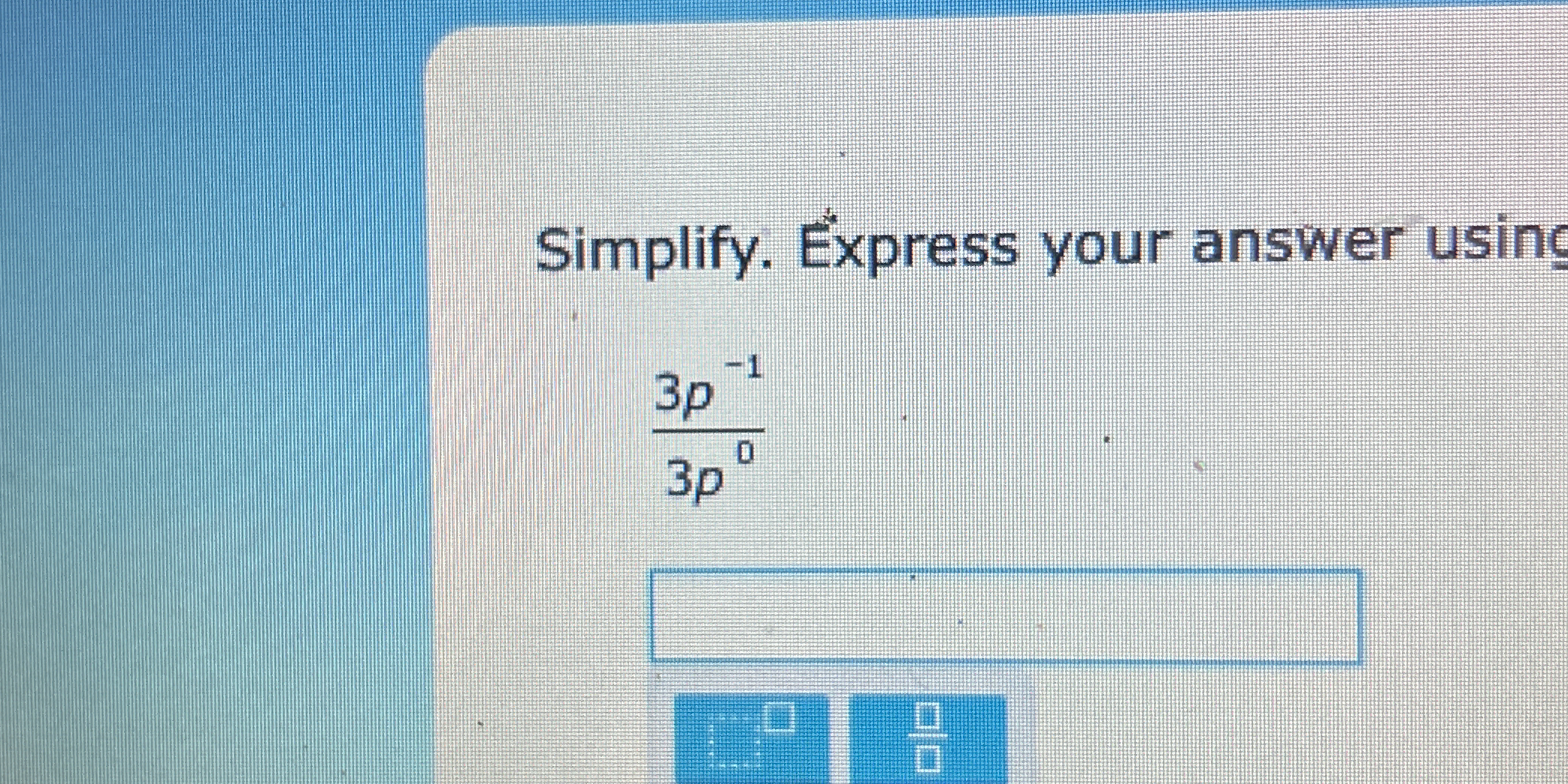
Simplify the expression 3p^{-1} / 3p^{0}.
Understand the Problem
The question asks us to simplify the expression ( \frac{3p^{-1}}{3p^{0}} ). To solve it, we will cancel out the common factors and apply the rules of exponents.
Answer
The simplified expression is \( \frac{1}{p} \).
Answer for screen readers
The simplified expression is ( \frac{1}{p} ).
Steps to Solve
-
Cancel out the common factors
In the expression ( \frac{3p^{-1}}{3p^{0}} ), we can cancel the common factor of 3 in the numerator and the denominator.
This simplifies to:
$$ \frac{p^{-1}}{p^{0}} $$ -
Apply the exponent rules
Now, we simplify the expression further using the properties of exponents. Recall that ( p^{0} = 1 ). The expression becomes:
$$ \frac{p^{-1}}{1} = p^{-1} $$ -
Convert to positive exponent
To express ( p^{-1} ) with a positive exponent, we can use the rule ( p^{-n} = \frac{1}{p^{n}} ).
Thus,
$$ p^{-1} = \frac{1}{p} $$
The simplified expression is ( \frac{1}{p} ).
More Information
The expression ( p^{-1} ) indicates the reciprocal of ( p ). Whenever you have a negative exponent, it can be re-written as a fraction with a positive exponent.
Tips
- Forgetting that ( p^{0} = 1 ) and incorrectly simplifying it.
- Not converting the negative exponent correctly into a positive one.
AI-generated content may contain errors. Please verify critical information