Simplify the expression: (12^8) / (12^5)
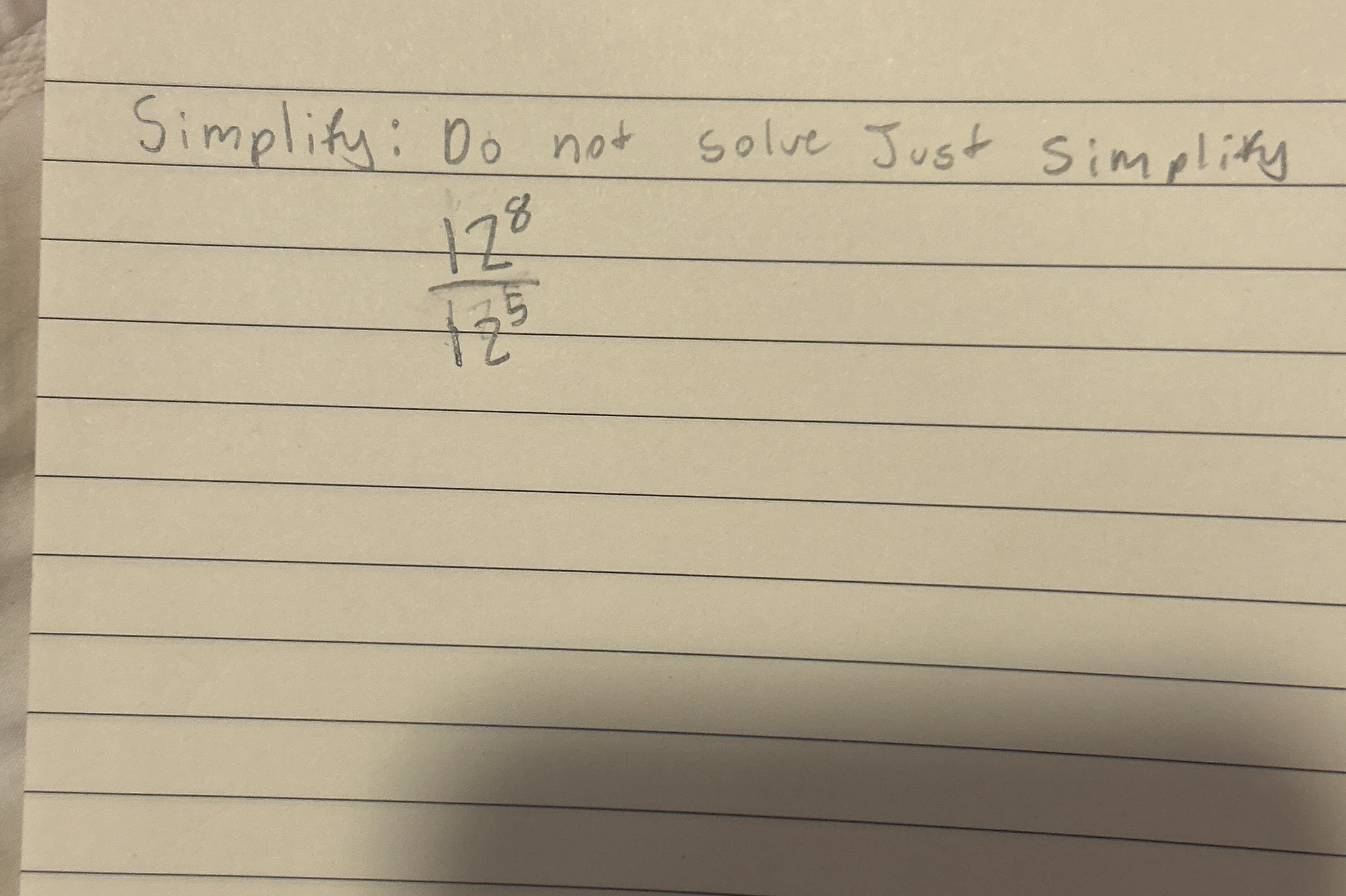
Understand the Problem
The question is asking to simplify the expression (12^8) / (12^5) without solving it completely. We need to apply the rules of exponents for simplification.
Answer
The simplified expression is \( 12^{3} \).
Answer for screen readers
The simplified expression is ( 12^{3} ).
Steps to Solve
- Identify the Quotient Rule of Exponents
The Quotient Rule states that when you divide two exponents with the same base, you subtract the exponents. For the expression ( \frac{12^8}{12^5} ), we will apply this rule.
- Apply the Quotient Rule
Using the Quotient Rule, we can simplify our expression as follows: $$ \frac{12^8}{12^5} = 12^{8-5} $$
- Simplify the Exponent
Now, simplify the exponent: $$ 12^{8-5} = 12^{3} $$
The simplified expression is ( 12^{3} ).
More Information
This simplification utilizes the Quotient Rule of exponents, which is beneficial in many areas of mathematics, especially when working with powers and roots.
Tips
- Not subtracting the exponents correctly: Be careful to always perform the subtraction correctly to avoid errors in the final exponent.
- Forgetting the base: Sometimes, students may forget to preserve the base (12 in this case) when simplifying.
AI-generated content may contain errors. Please verify critical information