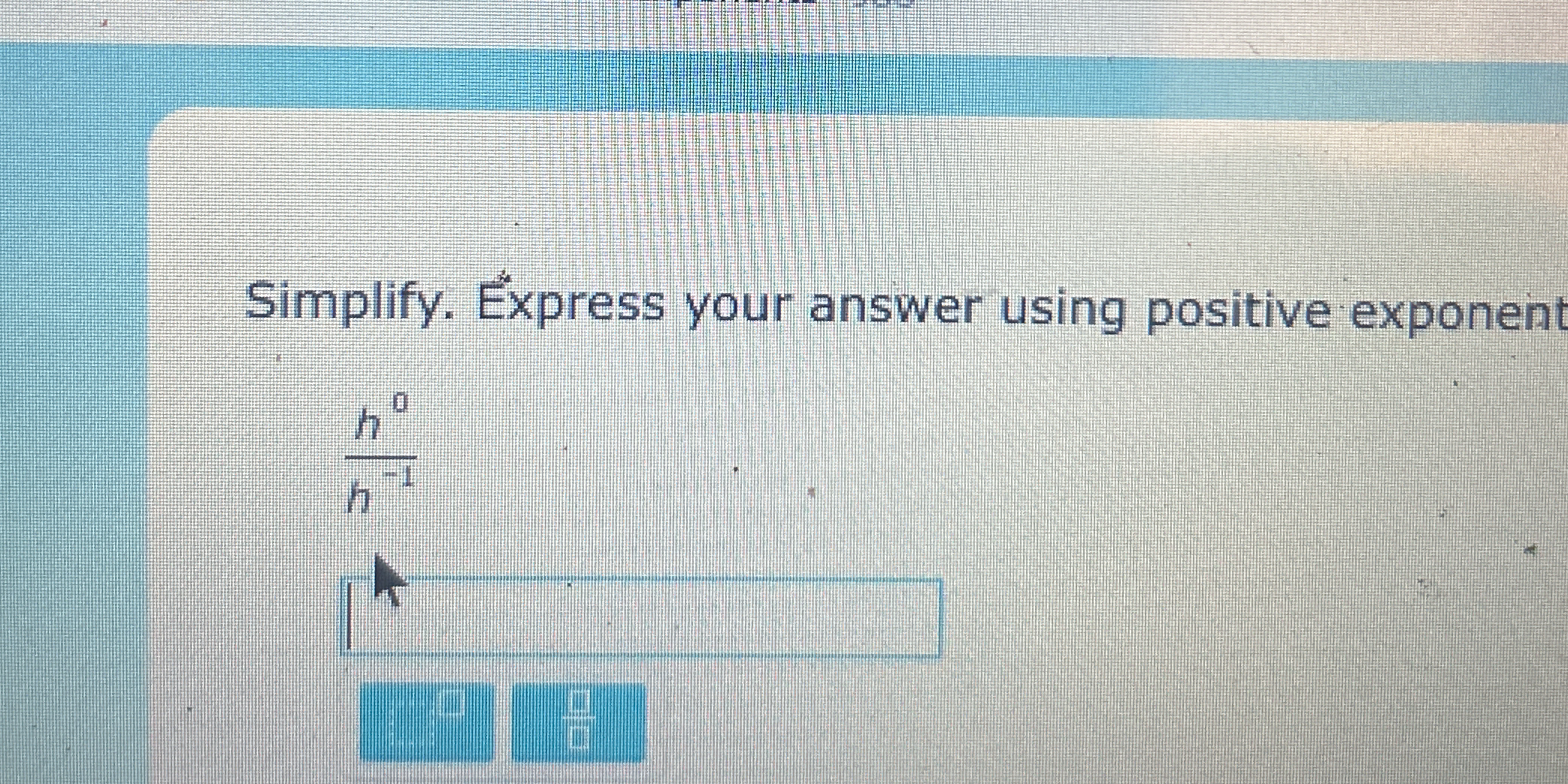
Simplify (h^0) / (h^-1) and express your answer using positive exponents.
Understand the Problem
The question is asking to simplify the expression (h^0) / (h^-1) and express the answer using only positive exponents.
Answer
The simplified expression is \( h \).
Answer for screen readers
The simplified expression is ( h ).
Steps to Solve
- Identify the expression to simplify
We start with the expression:
$$ \frac{h^0}{h^{-1}} $$
- Apply the zero exponent rule
Recall that any non-zero number raised to the power of 0 is equal to 1. Therefore:
$$ h^0 = 1 $$
Now our expression looks like this:
$$ \frac{1}{h^{-1}} $$
- Rewrite using the property of negative exponents
The property of negative exponents states that $h^{-n} = \frac{1}{h^n}$. Therefore,
$$ \frac{1}{h^{-1}} = h^{1} $$
- Final expression
After applying the negative exponent property, we find that:
$$ h^{1} = h $$
The simplified expression is ( h ).
More Information
This simplification utilized the properties of exponents, specifically about zero and negative exponents. Understanding these rules is crucial in algebra for simplifying expressions.
Tips
- A common mistake is forgetting that ( h^0 = 1 ) and wrongly assuming it remains as ( h ).
- Confusing how to handle negative exponents can lead to incorrect simplifications, so it’s important to always remember that ( h^{-n} = \frac{1}{h^n} ).
AI-generated content may contain errors. Please verify critical information