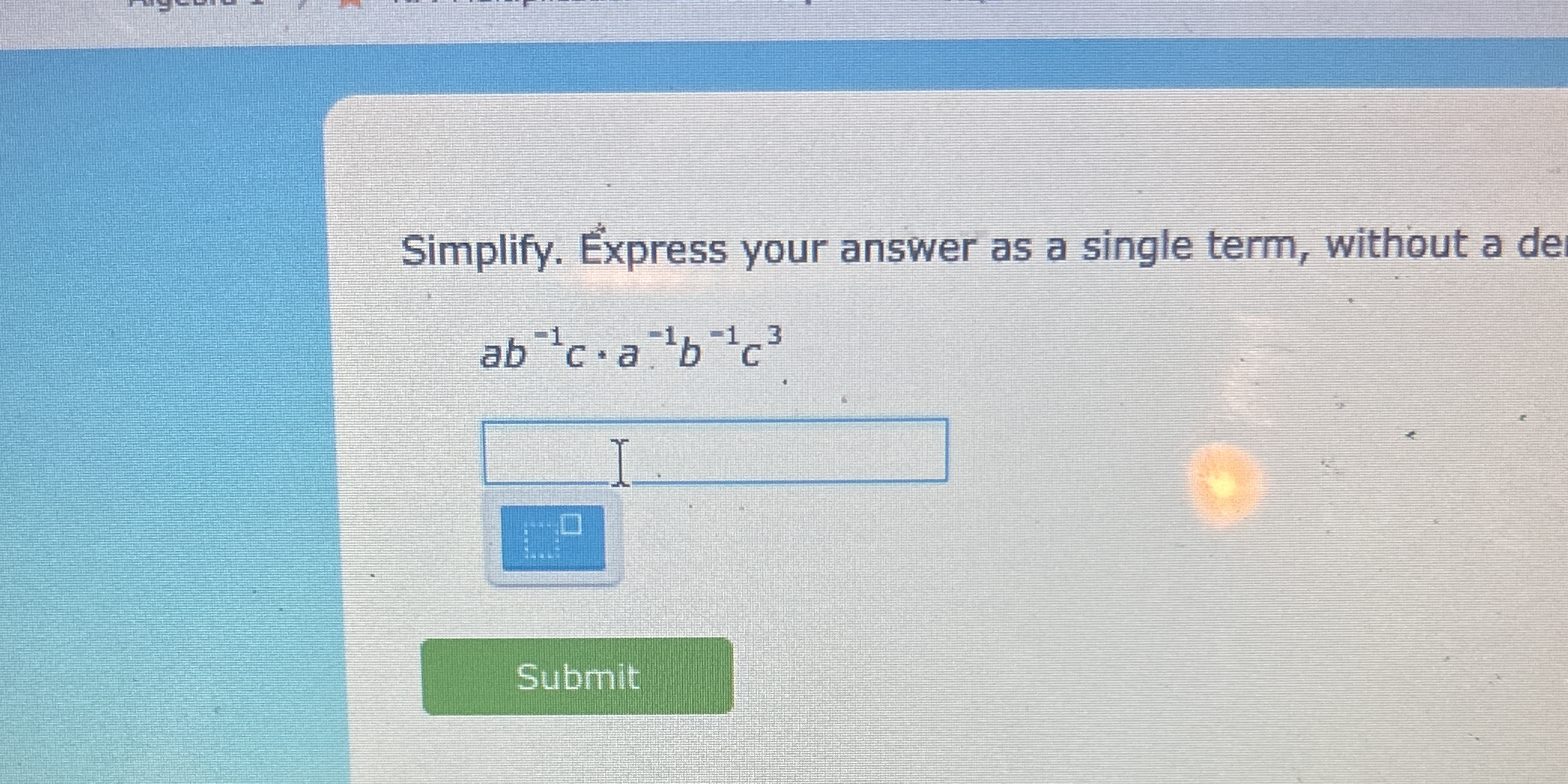
Simplify. Express your answer as a single term, without a denominator: ab^{-1}c^{-1}a^{-1}b^{-1}c^{3}.
Understand the Problem
The question is asking us to simplify the expression ab^{-1}c^{-1}a^{-1}b^{-1}c^{3}. We will focus on combining the similar terms and applying the rules of exponents to express it as a single term.
Answer
The simplified expression is \( b^{-2}c^{2} \).
Answer for screen readers
The simplified expression is ( b^{-2}c^{2} ).
Steps to Solve
- Identify the Expression We start with the expression:
$$ ab^{-1}c^{-1}a^{-1}b^{-1}c^{3} $$
- Rearrange and Group Terms We can rearrange the terms for clarity and combine like bases:
$$ (a \cdot a^{-1}) \cdot (b^{-1} \cdot b^{-1}) \cdot (c^{-1} \cdot c^{3}) $$
- Apply the Exponent Rules Now, apply the exponent rules:
- For the base (a):
$$ a \cdot a^{-1} = a^{1 - 1} = a^{0} = 1 $$
- For the base (b):
$$ b^{-1} \cdot b^{-1} = b^{-1 - 1} = b^{-2} $$
- For the base (c):
$$ c^{-1} \cdot c^{3} = c^{-1 + 3} = c^{2} $$
- Combine the Results Putting it all together gives:
$$ 1 \cdot b^{-2} \cdot c^{2} = b^{-2}c^{2} $$
- Final Expression The final simplified expression is:
$$ b^{-2}c^{2} $$
The simplified expression is ( b^{-2}c^{2} ).
More Information
The expression ( b^{-2}c^{2} ) shows that (b) appears in the denominator as (b^2), and (c) appears in the numerator squared. This combines the terms effectively while following the laws of exponents.
Tips
- One common mistake is forgetting that ( a^0 = 1 ), leading to an incorrect interpretation of the presence of a base in the final expression.
- Another mistake can be overlooking negative exponents, resulting in incorrect placement in the final answer.
AI-generated content may contain errors. Please verify critical information