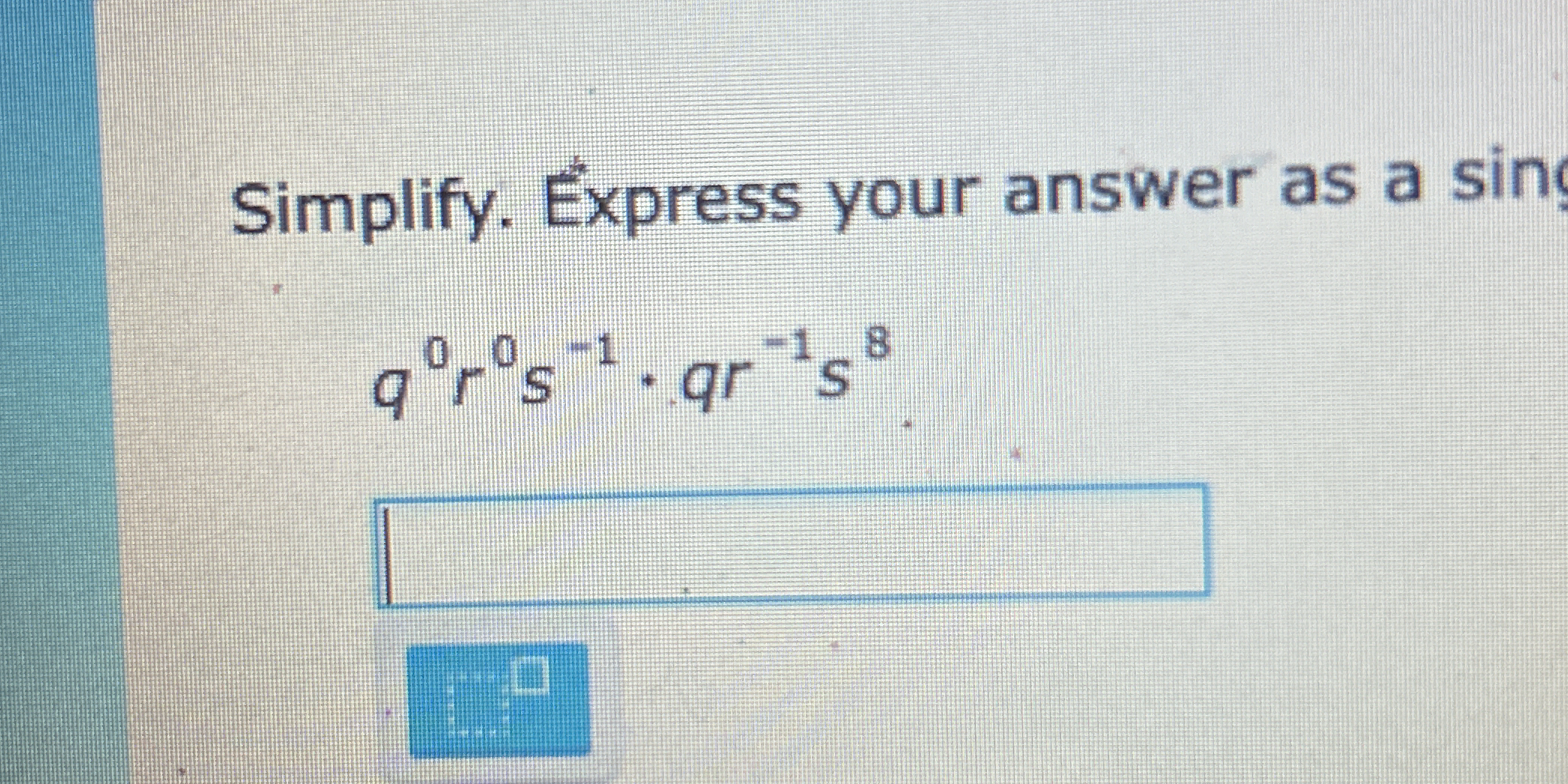
Simplify. Express your answer as a single term: q^0 r^(-1) s^(-1) · q^r s^(8)
Understand the Problem
The question is asking to simplify the expression q^0 r^(-1) s^(-1) · q^r s^(8) and express it as a single term. We will combine the like bases and apply the properties of exponents to simplify it.
Answer
The simplified expression is $\frac{q^r s^7}{r}$.
Answer for screen readers
The simplified expression is: $$ \frac{q^r s^7}{r} $$
Steps to Solve
- Simplify (q^0)
Using the rule that any number raised to the power of 0 is 1, we know: $$ q^0 = 1 $$ So the expression simplifies to: $$ 1 \cdot r^{-1} s^{-1} \cdot q^r s^8 $$
- Combine like bases
Now, we can combine the terms: $$ r^{-1} \cdot s^{-1} \cdot q^r \cdot s^8 = q^r \cdot r^{-1} \cdot s^{-1 + 8} $$
- Simplify the exponents for (s)
Calculate the exponent for (s): $$ s^{-1 + 8} = s^{7} $$ So now we have: $$ q^r \cdot r^{-1} \cdot s^7 $$
- Express as a single term
Combine the terms to get: $$ \frac{q^r \cdot s^7}{r} $$
The simplified expression is: $$ \frac{q^r s^7}{r} $$
More Information
This expression shows the relationship between the variables (q), (s), and (r) after applying the properties of exponents. The simplification process reveals the dependencies in exponentiation.
Tips
- Forgetting that (q^0) equals 1 and not incorporating it into the simplification process.
- Miscalculating the addition of exponents, specifically when combining the exponents of (s).
AI-generated content may contain errors. Please verify critical information