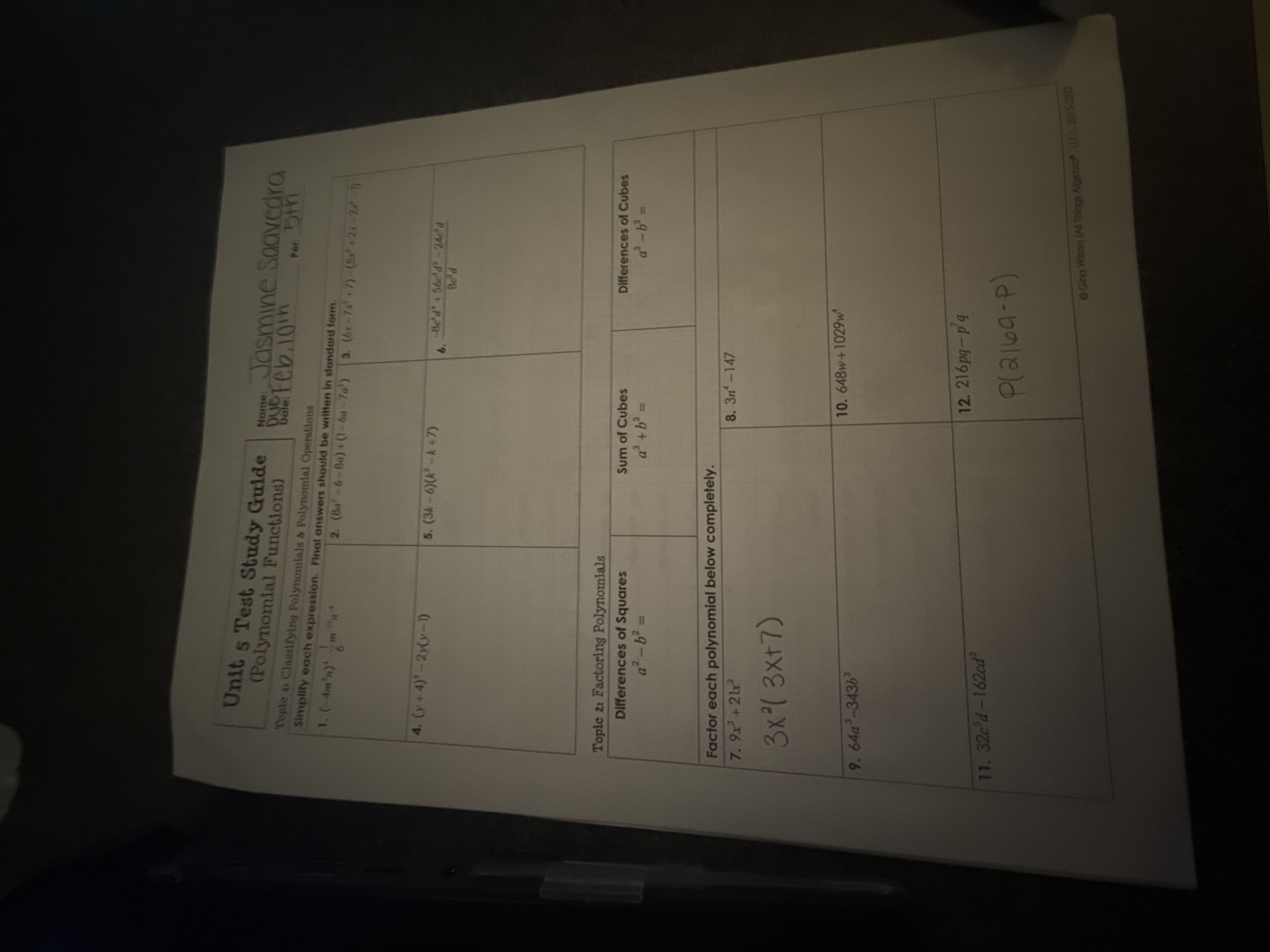
Simplify each expression and factor each polynomial below completely.

Steps to Solve

1. Simplify the first expression

   For the expression $\frac{-4m^3}{6} \cdot m^4$, first simplify the fraction: $$ \frac{-4}{6} = -\frac{2}{3} $$ Now, combine the powers of $m$: $$ m^3 \cdot m^4 = m^{3+4} = m^7 $$ Thus, the simplified expression is: $$ -\frac{2}{3} m^7 $$

2. Expand the second expression

   For $(8a^2 - 6a)(1 - 4a - 7a^2)$, use the distributive property (FOIL): [ 8a^2(1) + 8a^2(-4a) + 8a^2(-7a^2) - 6a(1) - 6a(-4a) - 6a(-7a^2) ]

   This gives: $$ 8a^2 - 32a^3 - 56a^4 - 6a + 24a^2 + 42a^3 $$

   Combine like terms: $$ -56a^4 + (8a^2 + 24a^2) + (-32a^3 + 42a^3) - 6a $$ So, $$ -56a^4 + 32a^2 + 10a^3 - 6a $$

3. Expand the third expression

   For $(6a - 7a^2 + 1)(5a^2 + 2a - 2)$: [ 6a(5a^2) + 6a(2a) + 6a(-2) - 7a^2(5a^2) - 7a^2(2a) - 7a^2(-2) + 1(5a^2) + 1(2a) + 1(-2) ] Combine like terms: $$ -35a^4 + 12a^3 + 6a + 5a^2 - 14a^2 - 6 $$

4. Simplify the fourth expression

   For $(x^4) - 2(x - 1)$: Distribute $-2$: $$ x^4 - 2x + 2 $$

5. Expand the fifth expression

   For $(3a - 6)(x^2 - x + 7)$: $$ 3a(x^2) - 3a(x) + 21a - 6(x^2) + 6(x) - 6(7) $$ Combine: $$ 3ax^2 - 3ax + 21a - 6x^2 + 6x - 42 $$

6. Combine like terms in the sixth expression

   For $8a^4 - 5a^4 - 2a^3$: $$ (8 - 5)a^4 - 2a^3 = 3a^4 - 2a^3 $$

7. Combine terms in the seventh expression

   For $9x^2 + 21x^2$: $$ (9 + 21)x^2 = 30x^2 $$

8. Simplify the eighth expression

   For $3^n - 147$, it remains as is: $$ 3^n - 147 $$

9. Factor the ninth expression

   For $64a^2 - 343b^3$, this is a difference of cubes: $$ (4a - 7b)(16a^2 + 28ab + 49b^2) $$

10. Combine like terms in the tenth expression

    For $648w + 1029w^n$, factor out $3w$: $$ 3w(216 + 343w^{n-1}) $$

11. Factor the eleventh expression

    For $32c^4 - 162c^3$, factor out $2c^3$: $$ 2c^3(16c - 81) $$

12. Factor the twelfth expression

    For $216pq - p^2q$, factor out $pq$: $$ pq(216 - p) $$