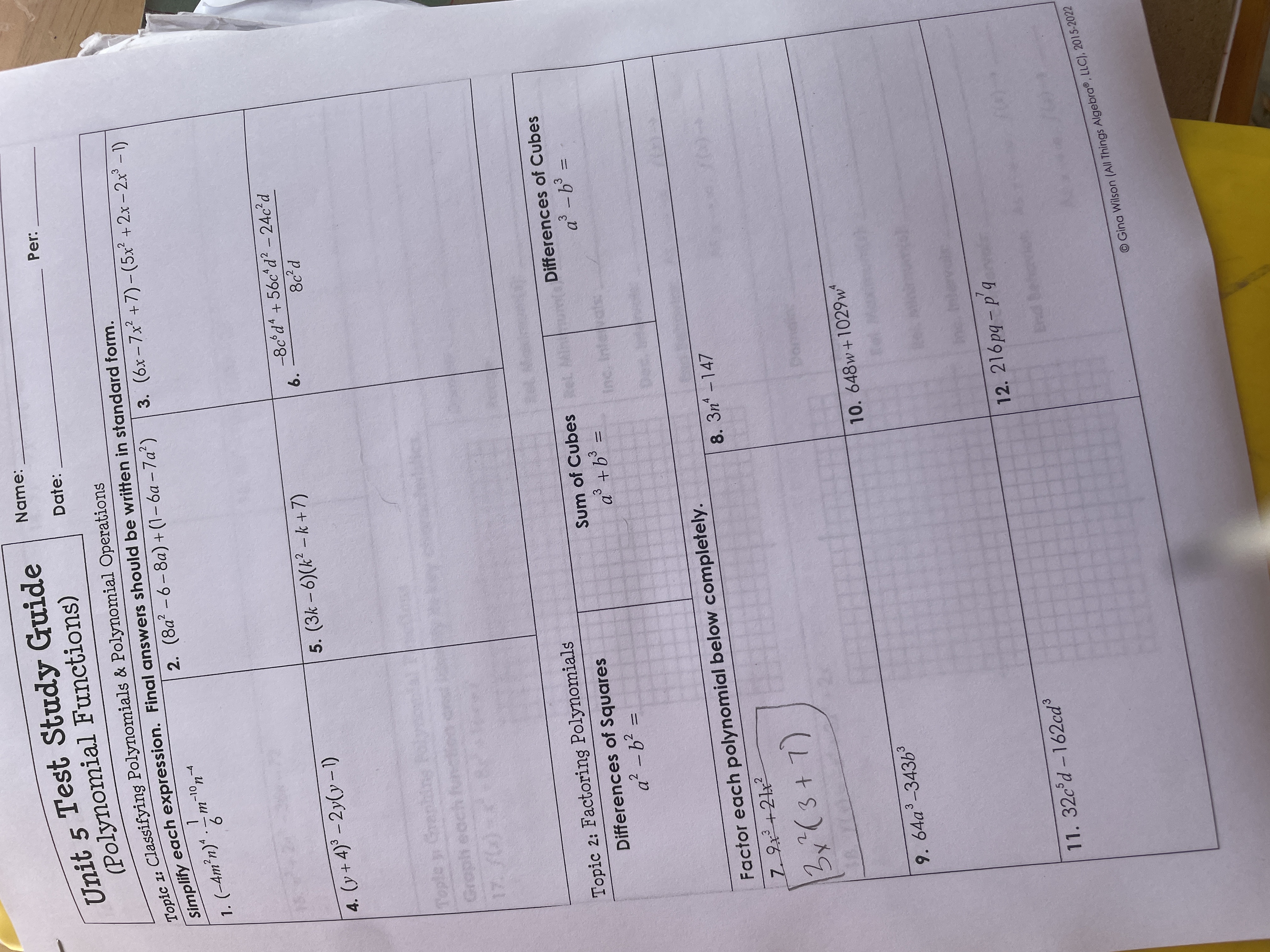
Simplify and factor the polynomial expressions provided in the study guide.

Steps to Solve

1. Simplifying Expression (1)

We need to simplify the expression:

$$ \frac{-4m^n}{6m^{10}n^4} $$

Divide the coefficients and apply the laws of exponents. The coefficients can be simplified as follows:

$$ \frac{-4}{6} = -\frac{2}{3} $$

For the variables, apply the exponent rule ( \frac{a^m}{a^n} = a^{m-n} ):

$$ \frac{m^n}{m^{10}} = m^{n - 10} $$ Thus, the entire expression simplifies to:

$$ -\frac{2}{3} m^{n-10} n^{-4} $$

Rewriting this in standard form leads to:

$$ -\frac{2}{3} \frac{m^{n-10}}{n^4} $$

2. Simplifying Expression (2)

Next, simplify:

$$ (8a^2 - 6a - 8a + 1 - 6a - 7a^2) $$

Combine like terms:

• Combine the ( a^2 ) terms:

$$ 8a^2 - 7a^2 = a^2 $$

• Combine the ( a ) terms:

$$ -6a - 8a - 6a = -20a $$

• The constant is ( 1 ).

So, we have:

$$ a^2 - 20a + 1 $$

3. Simplifying Expression (3)

For the expression:

$$ (6x - 7x^2 + 7) - (5x^2 + 2x - 2 - 1) $$

Distributing the negative:

$$ 6x - 7x^2 + 7 - 5x^2 - 2x + 2 + 1 $$

Now combine like terms:

• For ( x^2 ):

$$ -7x^2 - 5x^2 = -12x^2 $$

• For ( x ):

$$ 6x - 2x = 4x $$

• For the constant:

$$ 7 + 2 + 1 = 10 $$

Thus:

$$ -12x^2 + 4x + 10 $$

4. Simplifying Expression (4)

For:

$$ -8c^4d^4 + 56c^4d^2 - 24c^2d $$

Factor out the greatest common factor (GCF), which is ( -8c^2d ):

$$ -8c^2d(c^2d^3 - 7c^2d + 3) $$

5. Expression (5)

For:

$$ \frac{-8c^4d^4 + 56c^4d^2 - 24c^2d}{8d^2} $$

Divide each term:

$$ -c^4d^2 + 7c^4 - 3c^{-1} $$