Simplify 1/x + 3/x^3.
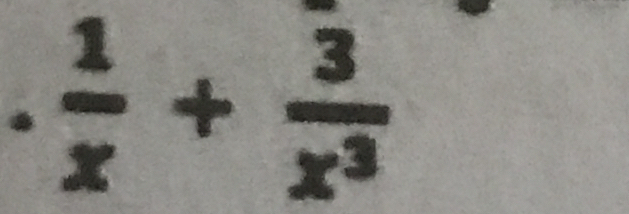
Understand the Problem
The question asks to simplify the addition of two algebraic fractions. The fractions are 1/x and 3/x^3. You need to find a common denominator, then add the numerators.
Answer
$\frac{x^2 + 3}{x^3}$
Answer for screen readers
$\frac{x^2 + 3}{x^3}$
Steps to Solve
-
Find the Least Common Denominator (LCD)
The denominators are $x$ and $x^3$. The LCD is $x^3$ since $x^3$ is divisible by $x$.
-
Rewrite the fractions with the LCD
We need to rewrite $\frac{1}{x}$ with the denominator $x^3$. To do this, we multiply the numerator and denominator by $x^2$:
$\frac{1}{x} \cdot \frac{x^2}{x^2} = \frac{x^2}{x^3}$
The second fraction, $\frac{3}{x^3}$, already has the LCD so we don't need to change it.
-
Add the fractions
Now we can add the two fractions since they have a common denominator:
$\frac{x^2}{x^3} + \frac{3}{x^3} = \frac{x^2 + 3}{x^3}$
$\frac{x^2 + 3}{x^3}$
More Information
The expression $\frac{x^2 + 3}{x^3}$ is already in its simplest form, as the numerator and denominator do not share any common factors. There might be values for $x$ that make the denominator zero, specifically $x = 0$, and thus the expression would be undefined.
Tips
A common mistake would be to try to cancel terms incorrectly. For example, one might try to cancel $x^2$ from the numerator and denominator of $\frac{x^2 + 3}{x^3}$, but this is not allowed because $x^2$ is not a factor of the entire numerator.
AI-generated content may contain errors. Please verify critical information