Simplify 15x^6 / 3x^-6
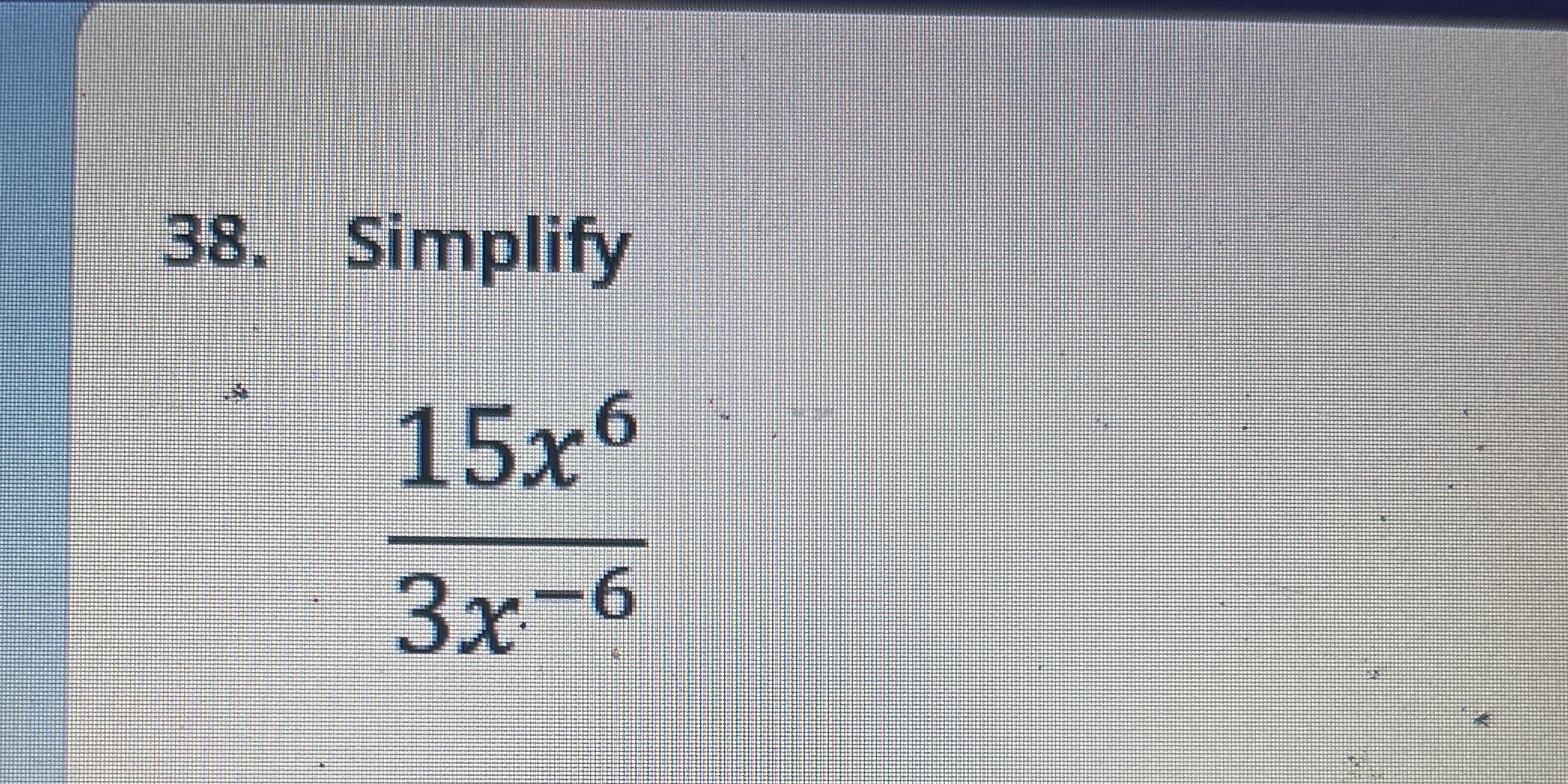
Understand the Problem
The question is asking to simplify the expression 15x^6 divided by 3x^-6. The high-level approach involves dividing the coefficients and applying the laws of exponents to simplify the variable parts.
Answer
The simplified expression is \( 5x^{12} \).
Answer for screen readers
The simplified expression is ( 5x^{12} ).
Steps to Solve
- Divide the coefficients
First, divide the numerical coefficients:
$$ \frac{15}{3} = 5 $$
- Apply the laws of exponents for the variable
Next, simplify the variable part using the quotient of powers rule. The rule states:
$$ \frac{x^a}{x^b} = x^{a-b} $$
In this case:
$$ x^{6 - (-6)} = x^{6 + 6} = x^{12} $$
- Combine the results
Now, combine the results from the coefficient division and variable simplification:
$$ \frac{15x^6}{3x^{-6}} = 5x^{12} $$
The simplified expression is ( 5x^{12} ).
More Information
Simplifying expressions is a fundamental skill in algebra, especially in dealing with polynomials and rational expressions. The quotient of powers rule is particularly useful for manipulating exponents.
Tips
- Forgetting to subtract the exponents correctly. Ensure you always use the formula ( a - (-b) ) when the exponent is negative.
- Not simplifying the coefficients before handling the variable part. Always deal with numbers first, then variables.
AI-generated content may contain errors. Please verify critical information