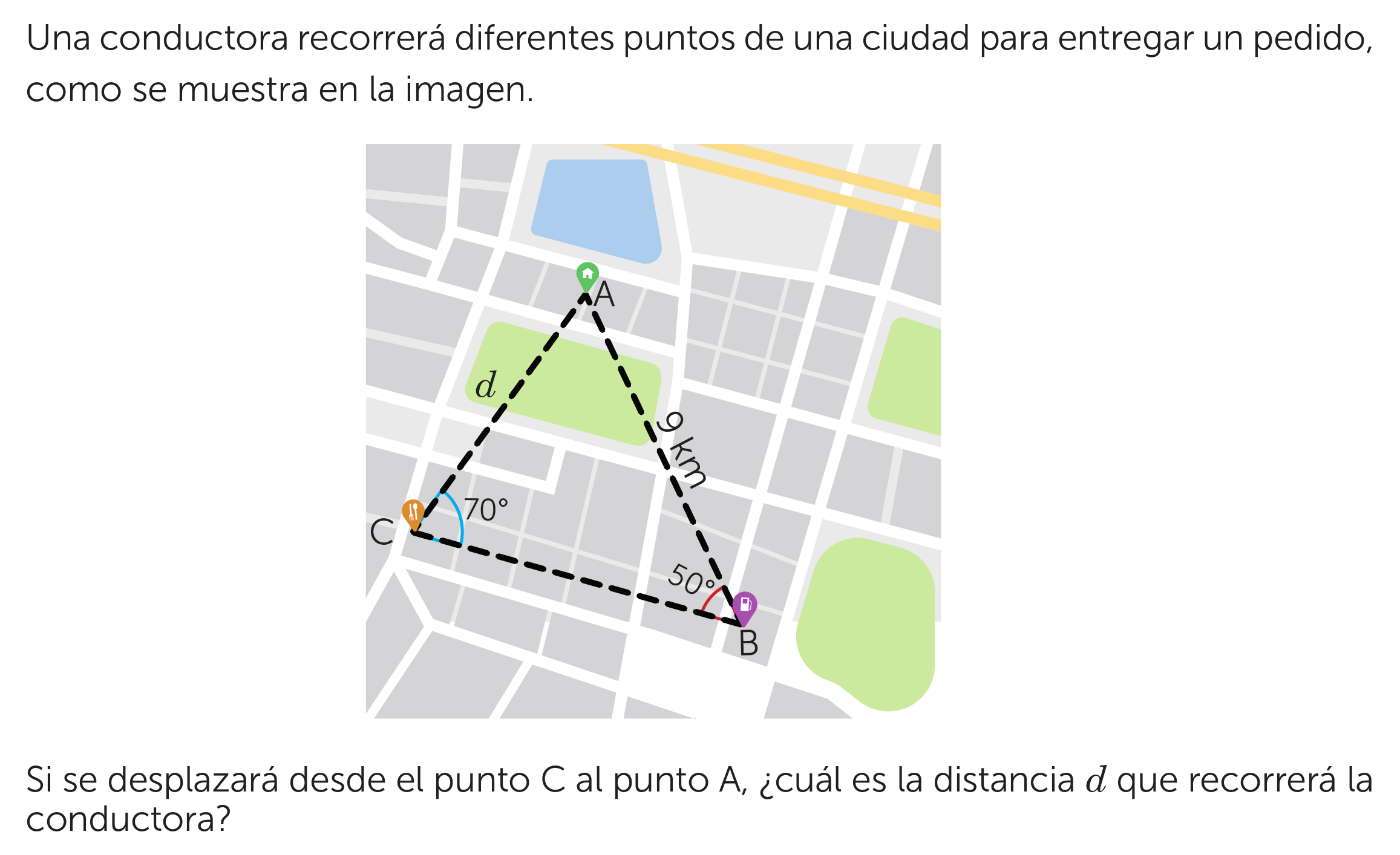
Si una conductora se desplazará desde el punto C al punto A, ¿cuál es la distancia d que recorrerá la conductora?
Understand the Problem
El problema presenta una situación en la que una conductora debe viajar entre diferentes puntos de una ciudad. Se proporciona un diagrama con tres puntos (A, B, y C) que forman un triángulo, con la distancia entre los puntos A y B dada como 9 km, el ángulo en el punto C como 70 grados, y el ángulo en el punto B como 50 grados. Se pide calcular la distancia 'd' entre los puntos C y A. Para resolverlo, podemos utilizar la ley de los senos o la ley de los cosenos, dependiendo de la información que tengamos y cómo la apliquemos.
Answer
$d \approx 7.96 \text{ km}$
Answer for screen readers
$d \approx 7.96 \text{ km}$
Steps to Solve
- Calculate the angle at point A
The sum of angles in any triangle is $180^\circ$. Therefore, the angle at point A can be calculated as follows: $$ \angle A = 180^\circ - \angle B - \angle C $$
$$ \angle A = 180^\circ - 50^\circ - 70^\circ = 60^\circ $$
- Apply the Law of Sines
The Law of Sines states that for any triangle: $$ \frac{a}{\sin A} = \frac{b}{\sin B} = \frac{c}{\sin C} $$ Where $a$, $b$, and $c$ are the side lengths opposite to angles $A$, $B$, and $C$, respectively.
- Set up the Law of Sines equation to find side $d$
In this case, we want to find the length of side $d$ (which is the distance between points C and A, and is opposite to angle B). We also know the length of the side opposite to angle A, which is 9 km. Therefore, we have: $$ \frac{d}{\sin B} = \frac{9}{\sin A} $$ $$ \frac{d}{\sin 50^\circ} = \frac{9}{\sin 60^\circ} $$
- Solve for $d$
Isolate d to be: $$ d = \frac{9 \cdot \sin 50^\circ}{\sin 60^\circ} $$
Using a calculator: $$ d = \frac{9 \cdot 0.766}{0.866} $$ $$ d \approx \frac{6.894}{0.866} \approx 7.96 \text{ km} $$
$d \approx 7.96 \text{ km}$
More Information
The Law of Sines is a fundamental trigonometric relationship applicable to all triangles, providing a direct link between the angles and the lengths of the sides.
Tips
A common mistake is using the Law of Cosines when the Law of Sines is more straightforward. Another common mistake is incorrectly identifying which side is opposite which angle. Lastly, calculator errors or incorrect rounding can lead to inaccurate results.
AI-generated content may contain errors. Please verify critical information