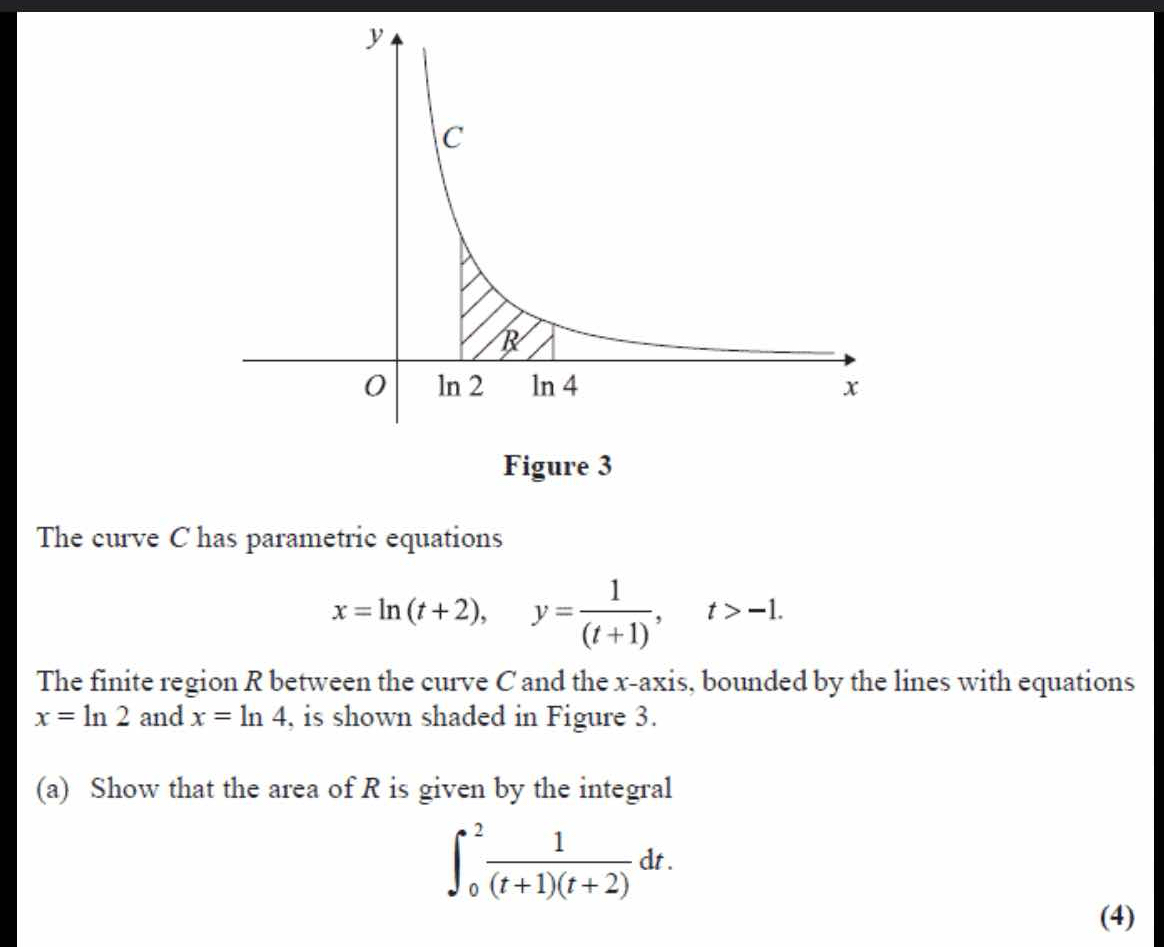
Show that the area of R is given by the integral ∫(from 0 to 2) of (1/((t+1)(t+2))) dt.

Steps to Solve

1. Identify the Parametric Equations

   The given parametric equations for the curve ( C ) are: [ x = \ln(t + 2), \quad y = \frac{1}{(t + 1)}, \quad t > -1. ]

2. Find the Limits of Integration

   We need to determine the values of ( t ) corresponding to the vertical lines ( x = \ln(2) ) and ( x = \ln(4) ).

   • For ( x = \ln(2) ): [ \ln(t + 2) = \ln(2) \implies t + 2 = 2 \implies t = 0. ]
   • For ( x = \ln(4) ): [ \ln(t + 2) = \ln(4) \implies t + 2 = 4 \implies t = 2. ]

3. Express the Area in Terms of ( t )

   The area ( A ) under the curve between ( t = 0 ) and ( t = 2 ) can be calculated by integrating the function ( y ) with respect to ( x ): [ A = \int_{0}^{2} y \frac{dx}{dt} , dt. ]

4. Calculate ( \frac{dx}{dt} )

   First, find ( \frac{dx}{dt} ): [ \frac{dx}{dt} = \frac{d}{dt}[\ln(t + 2)] = \frac{1}{t + 2}. ]

5. Substitute ( y ) and ( \frac{dx}{dt} ) into the Area Formula

   Substitute ( y ) and ( \frac{dx}{dt} ) into the area integral: [ A = \int_{0}^{2} \frac{1}{t + 1} \cdot \frac{1}{t + 2} , dt. ]

6. Final Formulation

   Hence, the area ( A ) can be expressed as: [ A = \int_{0}^{2} \frac{1}{(t + 1)(t + 2)} , dt, ] which is the required integral.