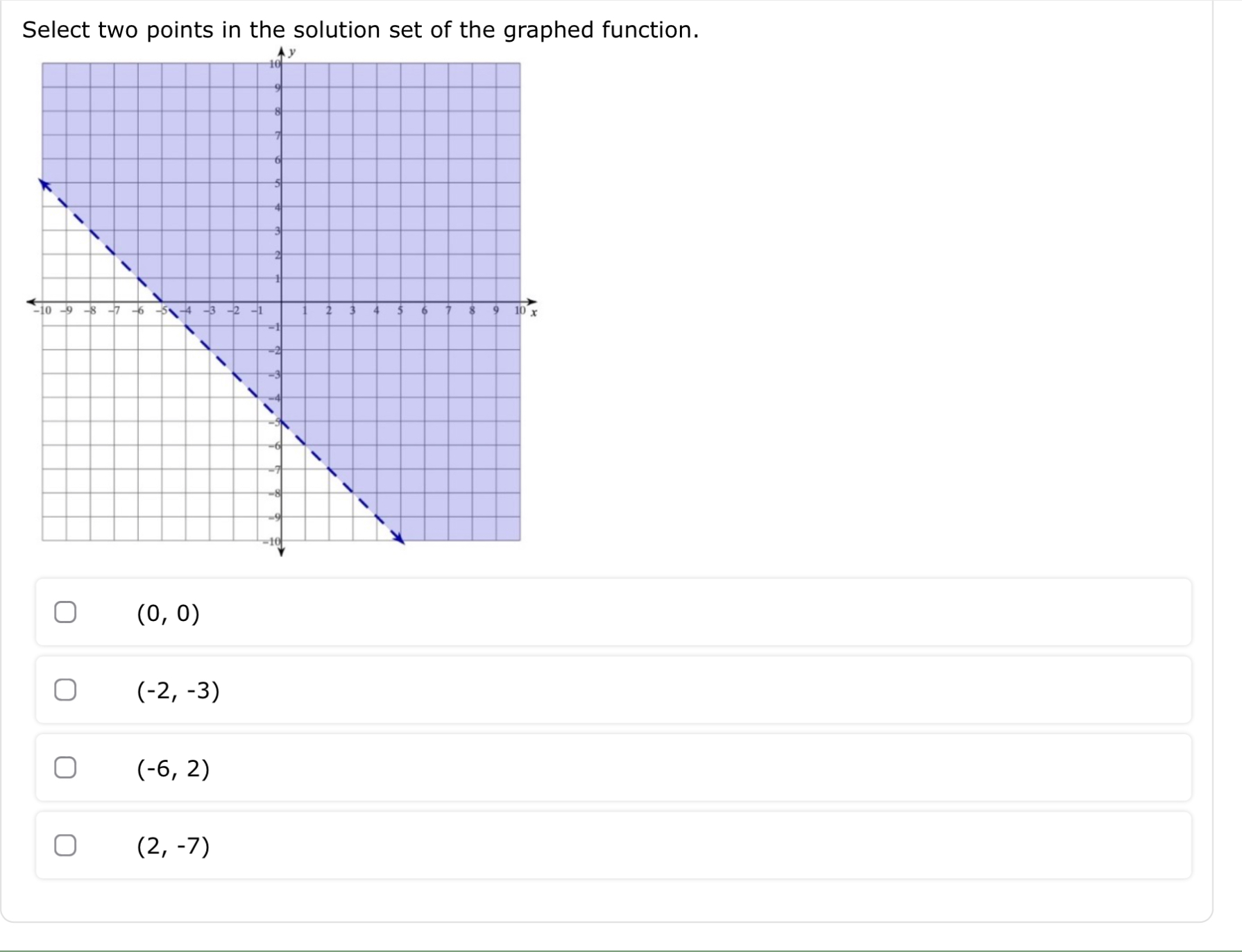
Select two points in the solution set of the graphed function.
Understand the Problem
The question is asking to identify two specific points that fall within the shaded solution set of the graph presented. The selected points must satisfy the inequality represented by the line in the graph.
Answer
The two points are $(-2, -3)$ and $(0, 0)$.
Answer for screen readers
The two points in the solution set of the graphed function are $(-2, -3)$ and $(0, 0)$.
Steps to Solve
-
Identify the Inequality The dashed line indicates that the inequality is linear. The line appears to be going downwards, suggesting it may look something like $y < mx + b$ for some values of $m$ and $b$. We can simplify it by using points on the line to find its equation.
-
Determine Points on the Line To find points on the line, let's identify two points:
- When $x = 0$, observe $y$ (intercept).
- When $y = 0$, observe $x$ (x-intercept). Based on the graph, if the line crosses the y-axis at $(0, 4)$ and the x-axis at $(4, 0)$, the equation of the line can be derived.
- Formulate the Equation The slope $m$ can be calculated as: $$ m = \frac{y_2 - y_1}{x_2 - x_1} = \frac{0 - 4}{4 - 0} = -1 $$
Using the slope and one point, the equation of the line is: $$ y = -x + 4$$
-
Identify the Shaded Region Since the line is dashed, the inequality is $y < -x + 4$. This indicates that all points below the line, including those in the shaded area, are solutions.
-
Test the Given Points We check each point to see if it satisfies the inequality:
- For $(0, 0)$: $0 < -0 + 4 \Rightarrow 0 < 4$ (True)
- For $(-2, -3)$: $-3 < -(-2) + 4 \Rightarrow -3 < 6$ (True)
- For $(-6, 2)$: $2 < -(-6) + 4 \Rightarrow 2 < 10$ (True)
- For $(2, -7)$: $-7 < -(2) + 4 \Rightarrow -7 < 2$ (True)
All points may seem valid, but we need only to select two that definitely lie in the shaded region.
The two points in the solution set of the graphed function are $(-2, -3)$ and $(0, 0)$.
More Information
Both selected points fall in the shaded area, which represents the solution to the inequality, confirming they satisfy the condition $y < -x + 4$.
Tips
- Confusing Dashed and Solid Lines: Be sure to remember that dashed lines indicate "less than" without including the boundary point.
- Assuming All Points Are Valid: Check each point against the inequality rather than assuming they all satisfy it.
AI-generated content may contain errors. Please verify critical information