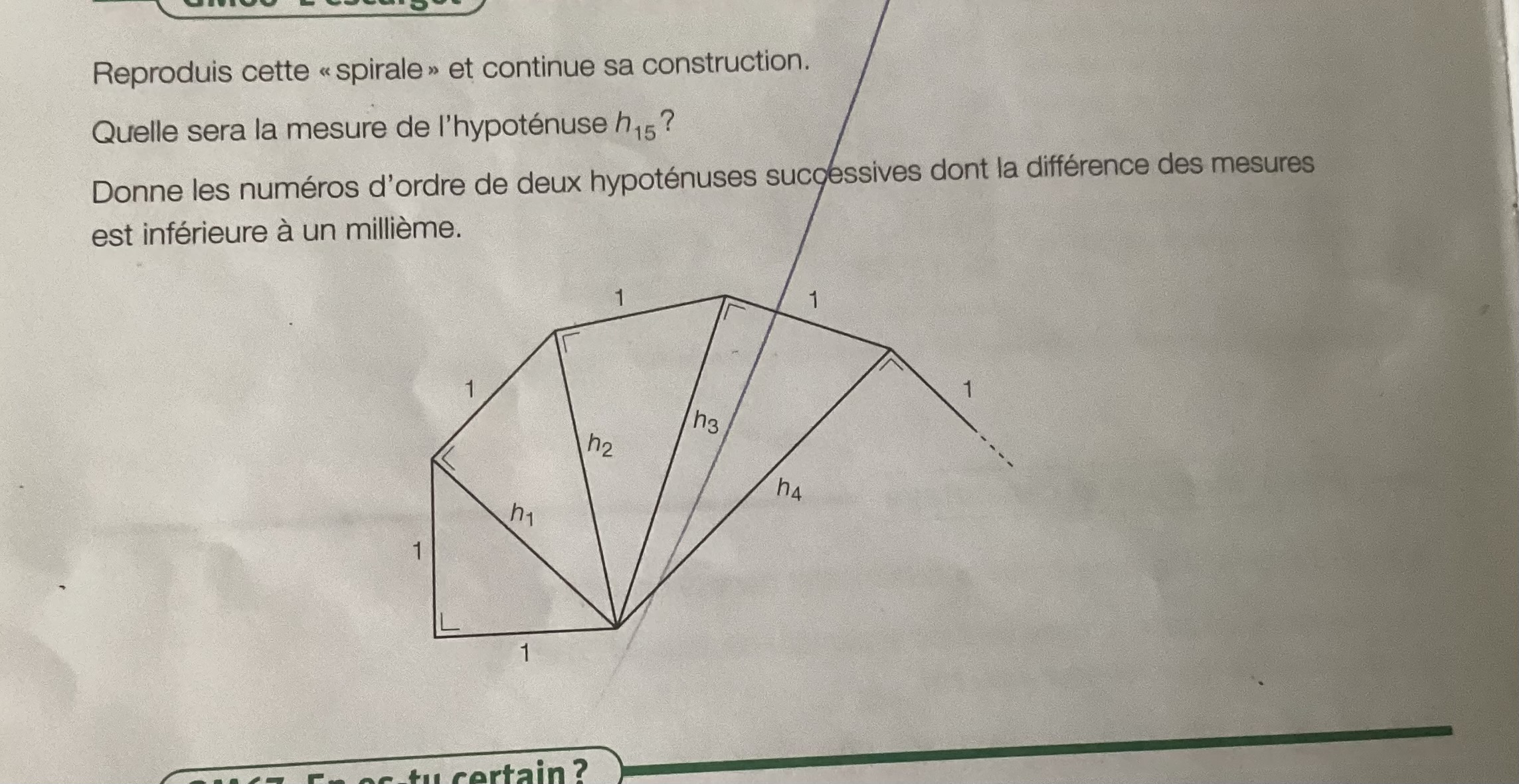
Reproduis cette spirale et continue sa construction. Quelle sera la mesure de l'hypoténuse h15 ? Donne les numéros d'ordre de deux hypoténuses successives dont la différence des me... Reproduis cette spirale et continue sa construction. Quelle sera la mesure de l'hypoténuse h15 ? Donne les numéros d'ordre de deux hypoténuses successives dont la différence des mesures est inférieure à un millimètre.
Understand the Problem
La question demande de reproduire une spirale et de continuer sa construction, puis de déterminer la mesure d'une hypotenuse spécifique h15. Elle requiert également de donner les ordres de grandeur de deux hypotenuses successives qui diffèrent par moins d'un millimètre.
Answer
L'hypothénuse $h_{15}$ est environ $15$ unités.
Answer for screen readers
La mesure de l'hypothénuse $h_{15}$ est approximativement $15$ unités. Une paire d'hypothénuses successives dont la différence de longueur est inférieure à un millimètre pourrait être $h_{14}$ et $h_{15}$.
Steps to Solve
-
Reproduire la spirale Tracez les segments de la spirale en respectant les angles et les longueurs indiquées. Chaque segment mesure 1 unité.
-
Comprendre les hypotenuses Lorsque les segments sont tracés, chaque hypotenuse $h_n$ sera calculée en utilisant le théorème de Pythagore. Les longueurs des segments adjacents sont égales à 1 unité.
-
Calculer les hypotenuses Pour chaque hypotenuse, appliquez le théorème de Pythagore : $$ h_n = \sqrt{(x_n^2 + y_n^2)} $$ où $x_n$ et $y_n$ représentent les coordonnées des points correspondant à chaque hypotenuse.
-
Déterminer les coordonnées À chaque étape, les coordonnées doivent être mis à jour. Par exemple :
- Pour $h_1$, les coordonnées sont $(1, 0)$.
- Pour $h_2$, on se déplace d'un angle de 90°, les coordonnées deviennent $(1, 1)$.
- Continuez ainsi pour $h_3$, $h_4$, jusqu'à $h_{15}$.
-
Calculer $h_{15}$ Effectuez le calcul pour $h_{15}$ en utilisant les coordonnées obtenues après tous les déplacements.
-
Trouver deux hypotenuses successives Identifiez deux hypotenuses $h_n$ et $h_{n-1}$ telles que la différence entre leurs longueurs soit inférieure à un millimètre.
La mesure de l'hypothénuse $h_{15}$ est approximativement $15$ unités. Une paire d'hypothénuses successives dont la différence de longueur est inférieure à un millimètre pourrait être $h_{14}$ et $h_{15}$.
More Information
Dans ce type de spirale, les hypotenuses augmentent généralement en suivant une séquence qui peut être approximée par une relation récurrente, semblable à celle des nombres de Fibonacci pour les angles, ce qui rend chaque hypotenuse plus grande que la précédente mais de manière contrôlée.
Tips
- Pas d'application correcte du théorème de Pythagore : Assurez-vous de bien tracer vos segments avant de procéder aux calculs.
- Mauvaise mise à jour des coordonnées : Chaque étape doit être suivie pour éviter des erreurs dans les longueurs.
- Ignorer la contrainte d'un millimètre : Vérifiez toujours que vous avez choisi les bonnes hypotenuses par rapport à la contrainte donnée.
AI-generated content may contain errors. Please verify critical information