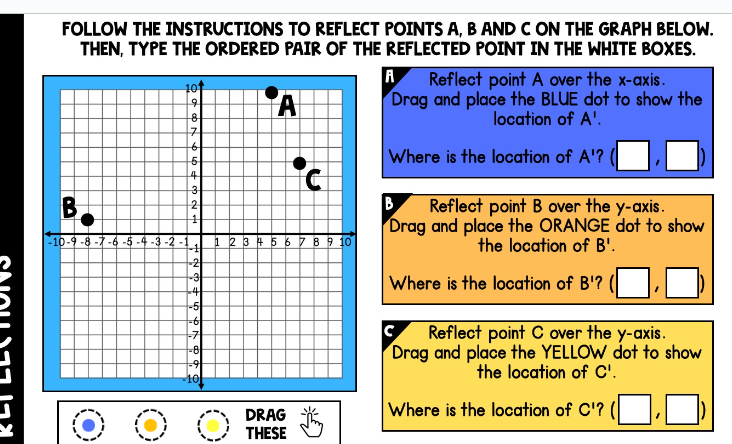
Reflect points A, B, and C on the graph below and type the ordered pair of the reflected point in the white boxes.
Understand the Problem
The question is asking how to reflect three points (A, B, and C) over specified axes on a graph and to identify their new coordinates after the reflections.
Answer
A': $(1, -5)$, B': $(3, 2)$, C': $(-4, -1)$.
Answer for screen readers
- The coordinates of A' are $(1, -5)$.
- The coordinates of B' are $(3, 2)$.
- The coordinates of C' are $(-4, -1)$.
Steps to Solve
-
Reflect Point A over the x-axis To reflect point A, take its original coordinates (x, y) and change the sign of the y-coordinate. If point A is at (1, 5), then: $$ A' = (1, -5) $$
-
Reflect Point B over the y-axis For point B, take its original coordinates (x, y) and change the sign of the x-coordinate. If point B is at (-3, 2), then: $$ B' = (3, 2) $$
-
Reflect Point C over the y-axis Similar to point B, take the coordinates of point C and change the sign of the x-coordinate. If point C is at (4, -1), then: $$ C' = (-4, -1) $$
- The coordinates of A' are $(1, -5)$.
- The coordinates of B' are $(3, 2)$.
- The coordinates of C' are $(-4, -1)$.
More Information
Point reflections are based on changing the signs of coordinates according to the axis over which you're reflecting. This preserves the distance from the axis but reverses the direction.
Tips
- Confusing which coordinate to change: Remember, reflecting over the x-axis changes the y-coordinate, while reflecting over the y-axis changes the x-coordinate.
- Forgetting to maintain the original points' positions in terms of their quadrants.
AI-generated content may contain errors. Please verify critical information