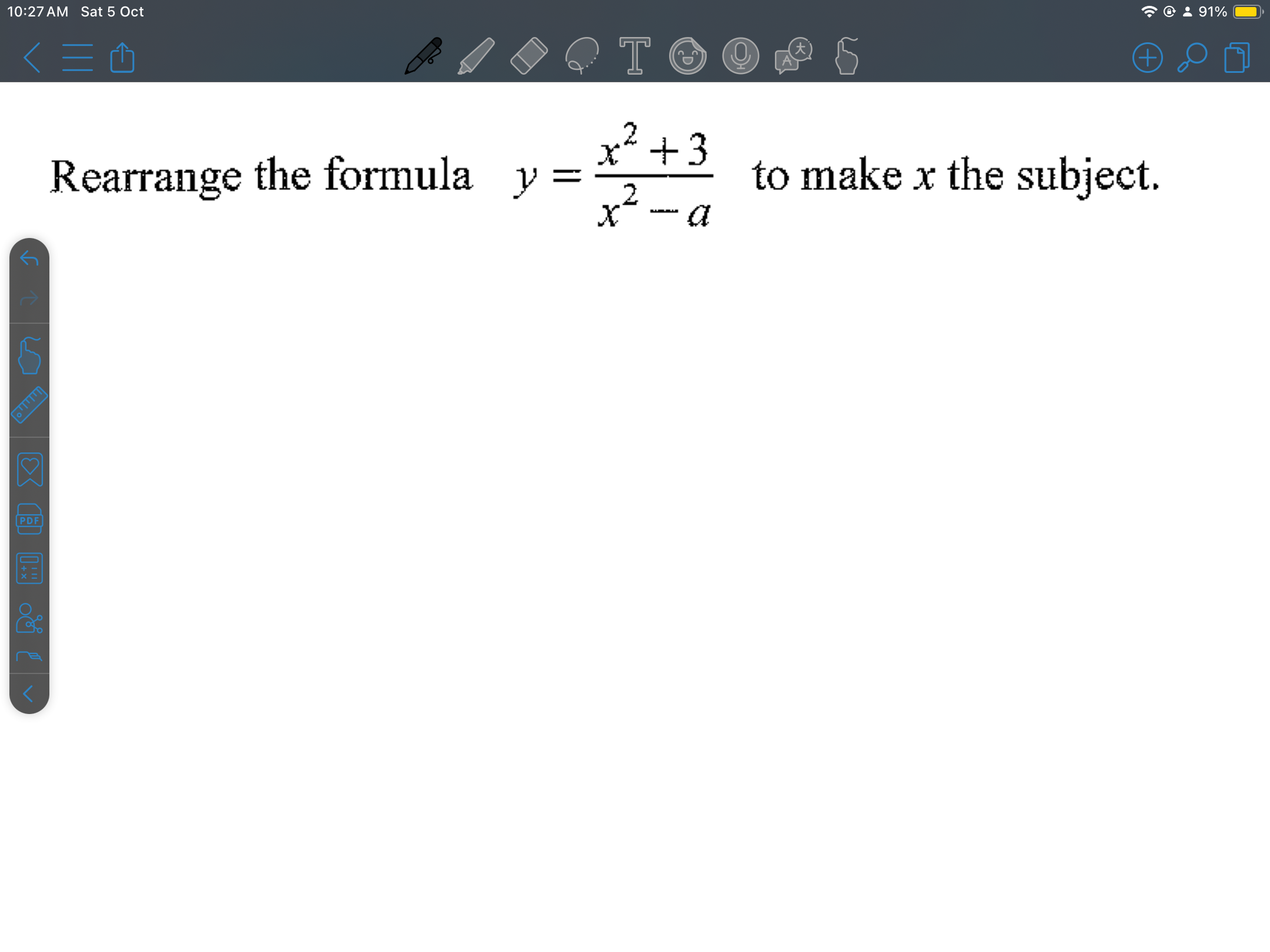
Rearrange the formula y = (x^2 + 3)/(x - a) to make x the subject.
Understand the Problem
The question is asking for a rearrangement of the given formula to isolate x as the subject. This involves algebraic manipulation and applying various algebraic rules to achieve the desired form.
Answer
$$ x = \frac{y \pm \sqrt{y^2 - 12 - 4ya}}{2} $$
Answer for screen readers
The rearranged formula for (x) is
$$ x = \frac{y \pm \sqrt{y^2 - 12 - 4ya}}{2} $$
Steps to Solve
- Multiply Both Sides by the Denominator
To eliminate the fraction, multiply both sides of the equation by the denominator (x - a):
$$ y(x - a) = x^2 + 3 $$
- Expand the Left Side
Distribute (y) on the left side:
$$ yx - ya = x^2 + 3 $$
- Rearrange the Equation
Move all terms to one side to set the equation to zero:
$$ x^2 - yx + (3 + ya) = 0 $$
- Use the Quadratic Formula
Now, recognize that the equation is a quadratic in (x) of the form (Ax^2 + Bx + C = 0) where (A = 1), (B = -y), and (C = 3 + ya). Apply the quadratic formula:
$$ x = \frac{-B \pm \sqrt{B^2 - 4AC}}{2A} $$
Substituting in the values:
$$ x = \frac{y \pm \sqrt{(-y)^2 - 4(1)(3 + ya)}}{2(1)} $$
- Simplify the Result
This simplifies to:
$$ x = \frac{y \pm \sqrt{y^2 - 12 - 4ya}}{2} $$
The rearranged formula for (x) is
$$ x = \frac{y \pm \sqrt{y^2 - 12 - 4ya}}{2} $$
More Information
This rearrangement of the formula enables you to express (x) in terms of (y) and other parameters. This is especially useful in solving equations where (x) is the unknown variable.
Tips
- Forgetting to properly distribute when multiplying both sides by the denominator.
- Not recognizing the quadratic form of the equation before applying the quadratic formula.
- Confusing signs when simplifying terms, especially during the quadratic calculation.
AI-generated content may contain errors. Please verify critical information