คำนวณวันที่ครบกำหนด, ดอกเบี้ย, และมูลค่าเมื่อครบกำหนดของตั๋วเงินแต่ละฉบับ โดยกำหนดให้ 1 ปีมี 360 วัน และแสดงผลลัพธ์เป็นทศนิยม 2 ตำแหน่ง ตามข้อมูลที่ให้มา คำนวณวันที่ครบกำหนด, ดอกเบี้ย, และมูลค่าเมื่อครบกำหนดของตั๋วเงินแต่ละฉบับ โดยกำหนดให้ 1 ปีมี 360 วัน และแสดงผลลัพธ์เป็นทศนิยม 2 ตำแหน่ง ตามข้อมูลที่ให้มา
Understand the Problem
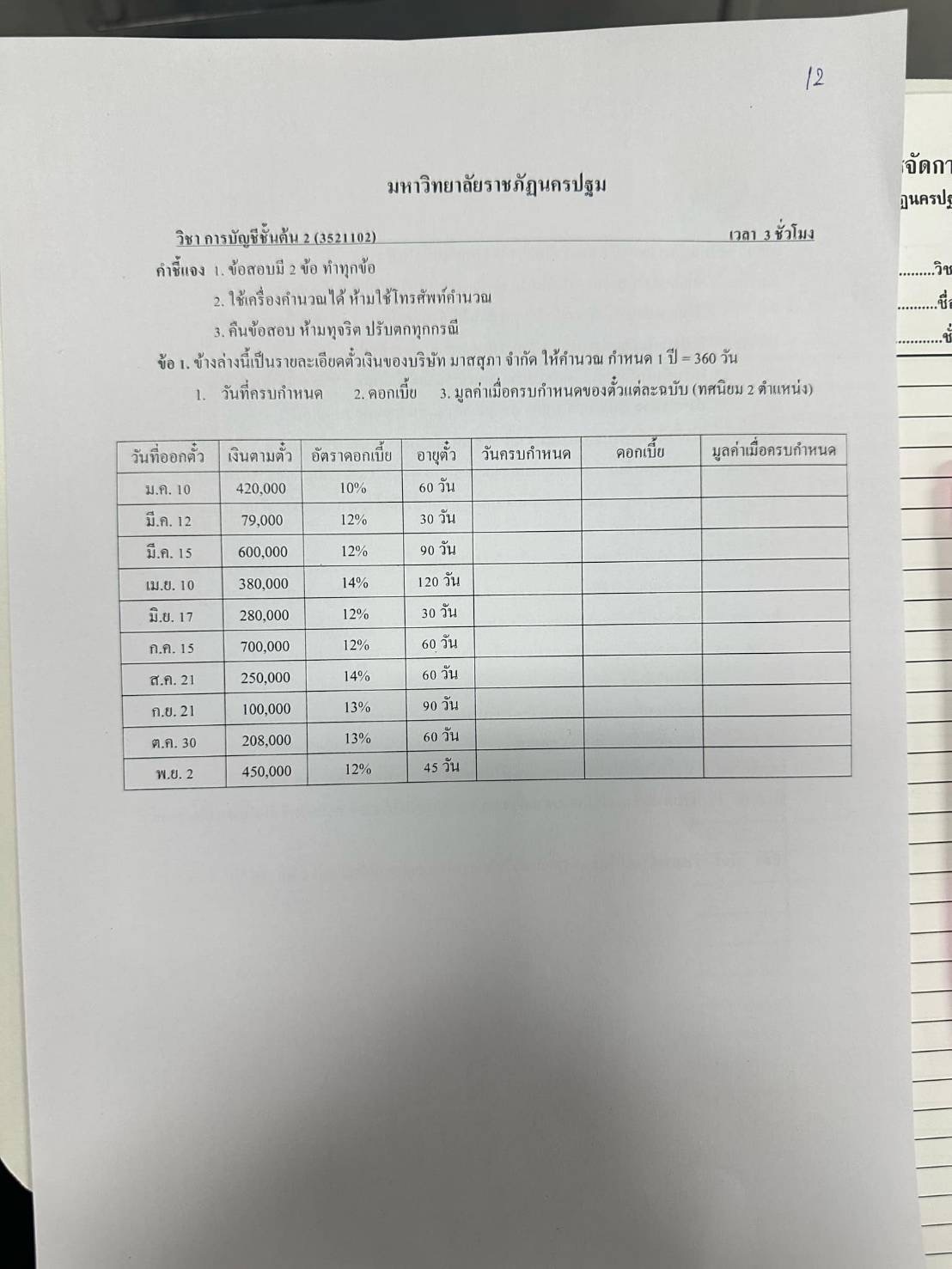
คำถามนี้เกี่ยวกับการคำนวณดอกเบี้ยและมูลค่าเมื่อครบกำหนดของตั๋วเงิน โดยมีรายละเอียดต่างๆ เช่น วันที่ออกตั๋ว, เงินตามตั๋ว, อัตราดอกเบี้ย, และอายุตั๋ว ให้คำนวณหาวันที่ครบกำหนด, ดอกเบี้ย, และมูลค่าเมื่อครบกำหนดของตั๋วแต่ละฉบับ โดยกำหนดให้ 1 ปีมี 360 วัน และแสดงผลลัพธ์เป็นทศนิยม 2 ตำแหน่ง
Answer
Here are the core calculations: $Interest = Principal \times Rate \times Time$ $Maturity Value = Principal + Interest$ See table in answer section for full results.
Answer for screen readers
Here are the calculated values for each bill, formatted to two decimal places:
| Issue Date | Face Value | Interest Rate | Term (Days) | Due Date | Interest | Maturity Value |
|---|---|---|---|---|---|---|
| Jan 10 | 420,000 | 10% | 60 | March 11 | 7,000.00 | 427,000.00 |
| Mar 12 | 79,000 | 12% | 30 | April 11 | 790.00 | 79,790.00 |
| Mar 15 | 600,000 | 12% | 90 | June 13 | 18,000.00 | 618,000.00 |
| Apr 10 | 380,000 | 14% | 120 | August 8 | 17,733.33 | 397,733.33 |
| Jun 17 | 280,000 | 12% | 30 | July 17 | 2,800.00 | 282,800.00 |
| Jul 15 | 700,000 | 12% | 60 | September 13 | 14,000.00 | 714,000.00 |
| Aug 21 | 250,000 | 14% | 60 | October 20 | 5,833.33 | 255,833.33 |
| Sep 21 | 100,000 | 13% | 90 | December 20 | 3,250.00 | 103,250.00 |
| Oct 30 | 208,000 | 13% | 60 | December 29 | 4,506.67 | 212,506.67 |
| Nov 2 | 450,000 | 12% | 45 | December 17 | 6,750.00 | 456,750.00 |
Steps to Solve
- Calculate the due date for each bill
To find the due date, add the term of the note to the issue date. Remember to consider the number of days in each month and that a year has 360 days. 2. Calculate the interest for each bill
The formula for calculating simple interest is: $Interest = Principal \times Rate \times Time$ Where:
- Principal is the face value of the bill.
- Rate is the annual interest rate.
- Time is the term of the note in years (days/360).
- Calculate the maturity value for each bill
The maturity value is the sum of the principal and the interest. $Maturity Value = Principal + Interest$
Now, let's apply these steps to each bill:
Bill 1: Issued Jan 10, 420,000, 10%, 60 days
- Due Date: Jan 10 + 60 days = March 11
- Interest: $420,000 \times 0.10 \times \frac{60}{360} = 7,000$
- Maturity Value: $420,000 + 7,000 = 427,000$
Bill 2: Issued Mar 12, 79,000, 12%, 30 days
- Due Date: Mar 12 + 30 days = April 11
- Interest: $79,000 \times 0.12 \times \frac{30}{360} = 790$
- Maturity Value: $79,000 + 790 = 79,790$
Bill 3: Issued Mar 15, 600,000, 12%, 90 days
- Due Date: Mar 15 + 90 days = June 13
- Interest: $600,000 \times 0.12 \times \frac{90}{360} = 18,000$
- Maturity Value: $600,000 + 18,000 = 618,000$
Bill 4: Issued Apr 10, 380,000, 14%, 120 days
- Due Date: Apr 10 + 120 days = August 8
- Interest: $380,000 \times 0.14 \times \frac{120}{360} = 17,733.33$
- Maturity Value: $380,000 + 17,733.33 = 397,733.33$
Bill 5: Issued Jun 17, 280,000, 12%, 30 days
- Due Date: Jun 17 + 30 days = July 17
- Interest: $280,000 \times 0.12 \times \frac{30}{360} = 2,800$
- Maturity Value: $280,000 + 2,800 = 282,800$
Bill 6: Issued Jul 15, 700,000, 12%, 60 days
- Due Date: Jul 15 + 60 days = September 13
- Interest: $700,000 \times 0.12 \times \frac{60}{360} = 14,000$
- Maturity Value: $700,000 + 14,000 = 714,000$
Bill 7: Issued Aug 21, 250,000, 14%, 60 days
- Due Date: Aug 21 + 60 days = October 20
- Interest: $250,000 \times 0.14 \times \frac{60}{360} = 5,833.33$
- Maturity Value: $250,000 + 5,833.33 = 255,833.33$
Bill 8: Issued Sep 21, 100,000, 13%, 90 days
- Due Date: Sep 21 + 90 days = December 20
- Interest: $100,000 \times 0.13 \times \frac{90}{360} = 3,250$
- Maturity Value: $100,000 + 3,250 = 103,250$
Bill 9: Issued Oct 30, 208,000, 13%, 60 days
- Due Date: Oct 30 + 60 days = December 29
- Interest: $208,000 \times 0.13 \times \frac{60}{360} = 4,506.67$
- Maturity Value: $208,000 + 4,506.67 = 212,506.67$
Bill 10: Issued Nov 2, 450,000, 12%, 45 days
- Due Date: Nov 2 + 45 days = December 17
- Interest: $450,000 \times 0.12 \times \frac{45}{360} = 6,750$
- Maturity Value: $450,000 + 6,750 = 456,750$
Here are the calculated values for each bill, formatted to two decimal places:
| Issue Date | Face Value | Interest Rate | Term (Days) | Due Date | Interest | Maturity Value |
|---|---|---|---|---|---|---|
| Jan 10 | 420,000 | 10% | 60 | March 11 | 7,000.00 | 427,000.00 |
| Mar 12 | 79,000 | 12% | 30 | April 11 | 790.00 | 79,790.00 |
| Mar 15 | 600,000 | 12% | 90 | June 13 | 18,000.00 | 618,000.00 |
| Apr 10 | 380,000 | 14% | 120 | August 8 | 17,733.33 | 397,733.33 |
| Jun 17 | 280,000 | 12% | 30 | July 17 | 2,800.00 | 282,800.00 |
| Jul 15 | 700,000 | 12% | 60 | September 13 | 14,000.00 | 714,000.00 |
| Aug 21 | 250,000 | 14% | 60 | October 20 | 5,833.33 | 255,833.33 |
| Sep 21 | 100,000 | 13% | 90 | December 20 | 3,250.00 | 103,250.00 |
| Oct 30 | 208,000 | 13% | 60 | December 29 | 4,506.67 | 212,506.67 |
| Nov 2 | 450,000 | 12% | 45 | December 17 | 6,750.00 | 456,750.00 |
More Information
The calculations are based on simple interest and a 360-day year, as specified in the problem description. The due dates are found by adding the term (in days) to the issue date.
Tips
A common mistake is using the actual number of days in a year (365 or 366) instead of the specified 360 days. Another mistake is incorrectly calculating the number of days between dates. Also, students often make rounding errors.
AI-generated content may contain errors. Please verify critical information