Prove the trigonometric identity 1 - tan²x / 1 + tan²x = 2cos²x - 1.
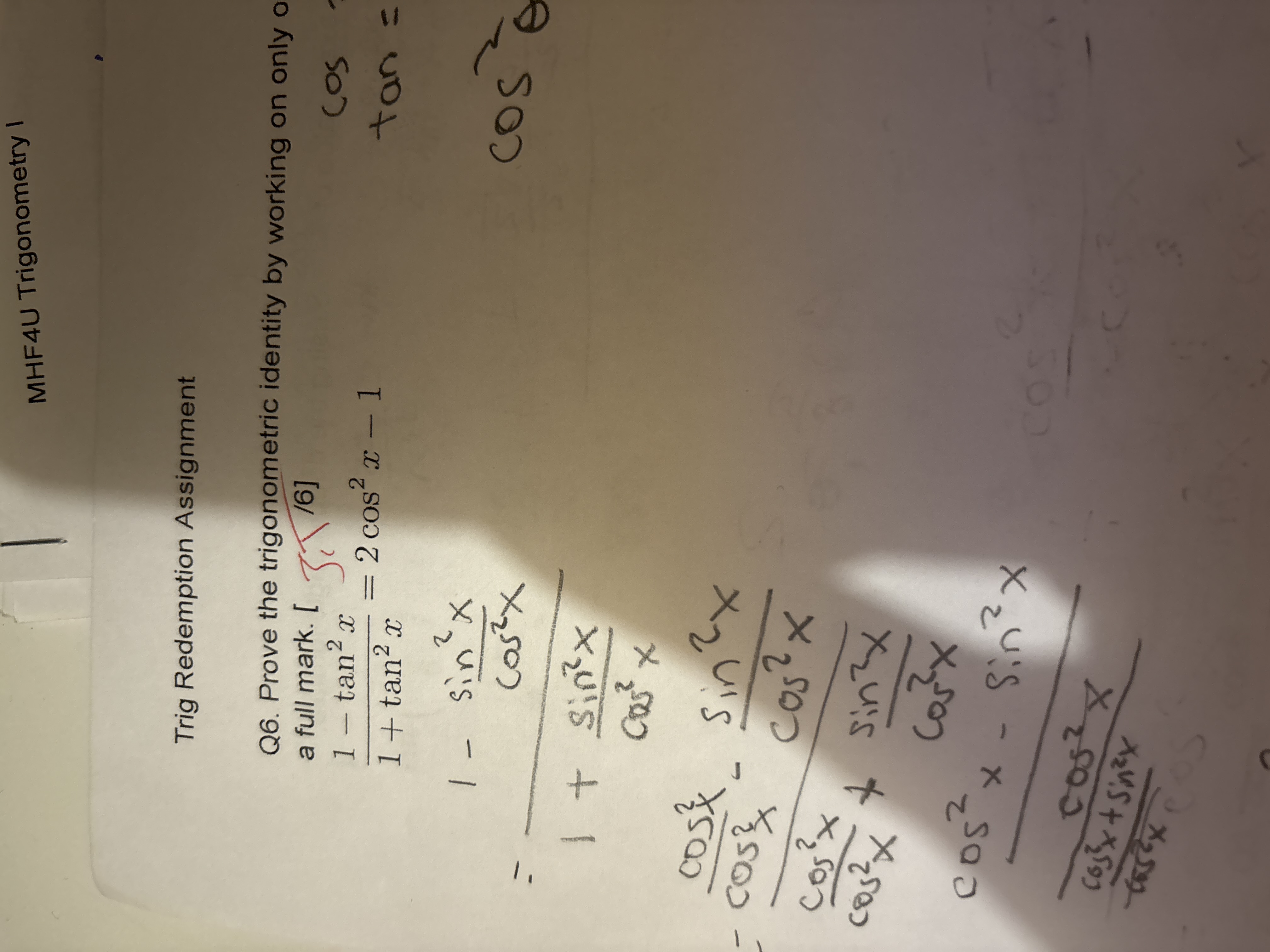
Understand the Problem
The question is asking to prove a trigonometric identity, specifically starting from one side of the equation and manipulating it to show that it equals the other side. This involves using trigonometric identities and algebraic manipulation.
Answer
The identity is proven as: $$ \frac{1 - \tan^2 x}{1 + \tan^2 x} = 2\cos^2 x - 1 $$
Answer for screen readers
The identity is proven as:
$$ \frac{1 - \tan^2 x}{1 + \tan^2 x} = 2\cos^2 x - 1 $$
Steps to Solve
- Start with the Left Side
Begin with the left side of the identity:
$$ LHS = \frac{1 - \tan^2 x}{1 + \tan^2 x} $$
- Substitute for $\tan^2 x$
Recall that $\tan^2 x = \frac{\sin^2 x}{\cos^2 x}$. Substitute this into the equation:
$$ LHS = \frac{1 - \frac{\sin^2 x}{\cos^2 x}}{1 + \frac{\sin^2 x}{\cos^2 x}} $$
- Combine the Fractions
Combine the numerators and denominators:
$$ LHS = \frac{\frac{\cos^2 x - \sin^2 x}{\cos^2 x}}{\frac{\cos^2 x + \sin^2 x}{\cos^2 x}} $$
- Simplify the Expression
Since $\cos^2 x + \sin^2 x = 1$, this simplifies to:
$$ LHS = \frac{\cos^2 x - \sin^2 x}{1} = \cos^2 x - \sin^2 x $$
- Use the Pythagorean Identity
Recall the double angle formula:
$$ \cos^2 x - \sin^2 x = 2\cos^2 x - 1 $$
- Conclusion
Thus, we have:
$$ LHS = 2\cos^2 x - 1 $$
Which shows that
$$ LHS = RHS $$
The identity is proven as:
$$ \frac{1 - \tan^2 x}{1 + \tan^2 x} = 2\cos^2 x - 1 $$
More Information
This identity connects the tangent function with cosine, demonstrating a relationship used in various trigonometric proofs and applications like deriving the double angle formulas.
Tips
- Confusing the identities: It's easy to mix up the signs when dealing with $\sin^2 x$ and $\cos^2 x$.
- Not simplifying the fractions properly; always double-check to simplify correctly.
AI-generated content may contain errors. Please verify critical information