Prove that ax² + bx + c = -b ± √(b² - 4ac) / 2a
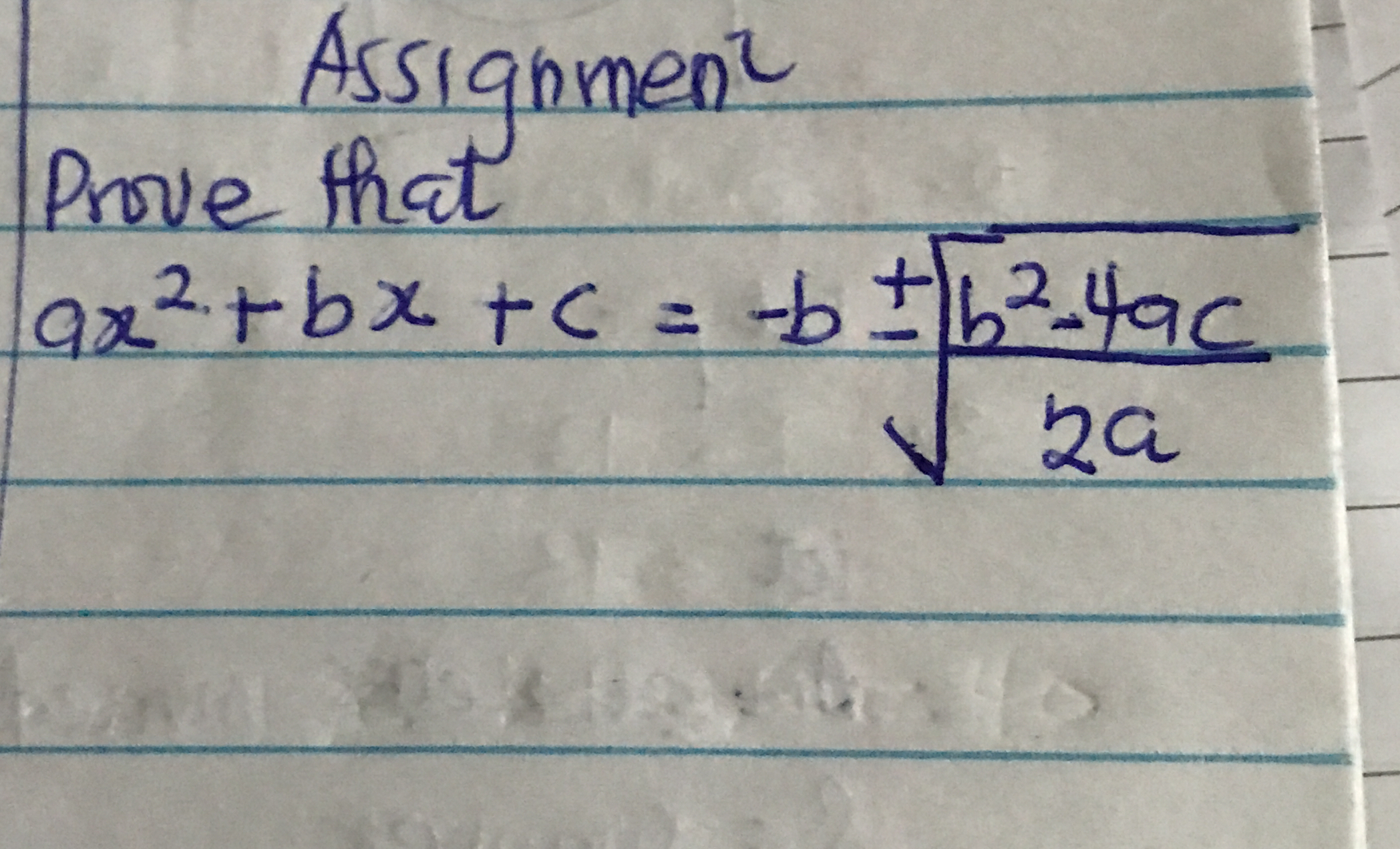
Understand the Problem
The question is requesting a proof for the equation relating to quadratic equations, particularly in the form of ax² + bx + c. It involves demonstrating that the expression equates to -b ± √(b² - 4ac) / 2a, which is part of the quadratic formula.
Answer
The quadratic formula is given by $x = \frac{-b \pm \sqrt{b^2 - 4ac}}{2a}$.
Answer for screen readers
The equation is proved as follows:
$$ x = \frac{-b \pm \sqrt{b^2 - 4ac}}{2a} $$
Steps to Solve
- Start with the standard quadratic equation
We begin with the quadratic equation in the standard form:
$$ ax^2 + bx + c = 0 $$
- Divide by 'a'
To simplify the equation, divide every term by $a$:
$$ x^2 + \frac{b}{a}x + \frac{c}{a} = 0 $$
- Rearrange the equation
Next, rearrange the equation to isolate the constant term:
$$ x^2 + \frac{b}{a}x = -\frac{c}{a} $$
- Complete the square
To complete the square on the left side, add $\left(\frac{b}{2a}\right)^2$ to both sides:
$$ x^2 + \frac{b}{a}x + \left(\frac{b}{2a}\right)^2 = -\frac{c}{a} + \left(\frac{b}{2a}\right)^2 $$
This simplifies to:
$$ \left(x + \frac{b}{2a}\right)^2 = -\frac{c}{a} + \frac{b^2}{4a^2} $$
- Combine terms
On the right side, find a common denominator and combine:
$$ \left(x + \frac{b}{2a}\right)^2 = \frac{b^2 - 4ac}{4a^2} $$
- Take the square root of both sides
Now, take the square root of both sides:
$$ x + \frac{b}{2a} = \pm \sqrt{\frac{b^2 - 4ac}{4a^2}} $$
- Solve for x
This can be rewritten as:
$$ x + \frac{b}{2a} = \frac{\pm \sqrt{b^2 - 4ac}}{2a} $$
Finally, isolate $x$:
$$ x = -\frac{b}{2a} \pm \frac{\sqrt{b^2 - 4ac}}{2a} $$
So,
$$ x = \frac{-b \pm \sqrt{b^2 - 4ac}}{2a} $$
The equation is proved as follows:
$$ x = \frac{-b \pm \sqrt{b^2 - 4ac}}{2a} $$
More Information
This formula is known as the quadratic formula, which provides the solutions to any quadratic equation of the form $ax^2 + bx + c = 0$. It allows us to find the roots (or x-intercepts) of the quadratic function.
Tips
- Forgetting to divide by 'a': Many students skip this step, which leads to incorrect transformations.
- Incorrectly completing the square: This can happen if adding the squared term isn't done correctly, leading to errors.
- Misplacing the negative sign during rearrangement: Ensure that the negative sign from $-c/a$ is accurately maintained throughout the steps.
AI-generated content may contain errors. Please verify critical information