Prove each identity. a) cos x tan^3 x = sin x tan^2 x b) sin^2 θ + cos^4 θ = cos^2 θ + sin^4 θ c) (sin x + cos x)(tan^2 x + 1)/tan x = 1/cos x + 1/sin x d) tan^2 β + cos^2 β + sin^... Prove each identity. a) cos x tan^3 x = sin x tan^2 x b) sin^2 θ + cos^4 θ = cos^2 θ + sin^4 θ c) (sin x + cos x)(tan^2 x + 1)/tan x = 1/cos x + 1/sin x d) tan^2 β + cos^2 β + sin^2 β = 1/cos^2 β e) sin(π/4 + x) + sin(π/4 - x) = √2 cos x f) sin(π/2 - x) cot(π/2 + x) = -sin x
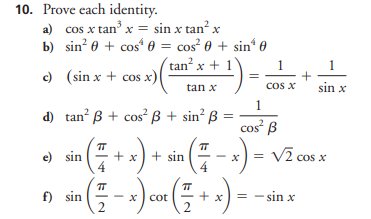
Understand the Problem
The question is asking to prove specific trigonometric identities step by step. Each item listed follows a format where one side of an equation must be shown to equal the other by manipulating the expressions using trigonometric identities.
Answer
a) $\cos x \tan^3 x = \sin x \tan^2 x$ b) $\sin^2 \theta + \cos^4 \theta = \cos^2 \theta + \sin^4 \theta$ c) $(\sin x + \cos x) \frac{\tan^2 x + 1}{\tan x} = \frac{1}{\cos x} + \frac{1}{\sin x}$ d) $\tan^2 \beta + \cos^2 \beta + \sin^2 \beta = \frac{1}{\cos^2 \beta}$ e) $\sin\left(\frac{\pi}{4} + x\right) + \sin\left(\frac{\pi}{4} - x\right) = \sqrt{2}\cos x + \sqrt{2}\sin x$ f) $\sin\left(\frac{\pi}{2} - x\right) \cot\left(\frac{\pi}{2} + x\right) = -\sin x$
Answer for screen readers
a) $\cos x \tan^3 x = \sin x \tan^2 x$
b) $\sin^2 \theta + \cos^4 \theta = \cos^2 \theta + \sin^4 \theta$
c) $(\sin x + \cos x) \frac{\tan^2 x + 1}{\tan x} = \frac{1}{\cos x} + \frac{1}{\sin x}$
d) $\tan^2 \beta + \cos^2 \beta + \sin^2 \beta = \frac{1}{\cos^2 \beta}$
e) $\sin\left(\frac{\pi}{4} + x\right) + \sin\left(\frac{\pi}{4} - x\right) = \sqrt{2}\cos x + \sqrt{2}\sin x$
f) $\sin\left(\frac{\pi}{2} - x\right) \cot\left(\frac{\pi}{2} + x\right) = -\sin x$
Steps to Solve
- Proof for part (a)
Start with the left-hand side:
$$ \text{LHS} = \cos x \tan^3 x $$
Recall that $\tan x = \frac{\sin x}{\cos x}$, so
$$ \tan^3 x = \frac{\sin^3 x}{\cos^3 x} $$
Thus,
$$ \text{LHS} = \cos x \cdot \frac{\sin^3 x}{\cos^3 x} = \frac{\sin^3 x}{\cos^2 x} $$
Now, rewrite the right-hand side:
$$ \text{RHS} = \sin x \tan^2 x = \sin x \cdot \frac{\sin^2 x}{\cos^2 x} = \frac{\sin^3 x}{\cos^2 x} $$
This confirms that $\text{LHS} = \text{RHS}$.
- Proof for part (b)
Start with the left-hand side:
$$ \text{LHS} = \sin^2 \theta + \cos^4 \theta $$
Use the Pythagorean identity $\sin^2 \theta + \cos^2 \theta = 1$, so
$$ \text{LHS} = \cos^2 \theta + \cos^4 \theta = \cos^2 \theta(1 + \cos^2 \theta) $$
For the right-hand side:
$$ \text{RHS} = \cos^2 \theta + \sin^4 \theta = \cos^2 \theta + (1 - \cos^2 \theta)^2 $$
Expand to find:
$$ \text{RHS} = \cos^2 \theta + 1 - 2\cos^2 \theta + \cos^4 \theta = 1 - \cos^2 \theta + \cos^4 \theta $$
This shows $\text{LHS} = \text{RHS}$.
- Proof for part (c)
Starting with:
$$ \text{LHS} = ( \sin x + \cos x ) \frac{\tan^2 x + 1}{\tan x} $$
Use the identity $\tan^2 x + 1 = \sec^2 x$, thus:
$$ \text{LHS} = ( \sin x + \cos x ) \frac{\sec^2 x}{\tan x} $$
Express $\sec^2 x$ as $\frac{1}{\cos^2 x}$ and $\tan x$ as $\frac{\sin x}{\cos x}$:
$$ \text{LHS} = ( \sin x + \cos x ) \frac{1/\cos^2 x}{\sin x/\cos x} = \frac{(\sin x + \cos x) \cos x}{\sin x} $$
Simplifying gives:
$$ \frac{\sin x + \cos x}{\sin x \cos x} $$
Match with right-hand side:
$$ \text{RHS} = \frac{1}{\cos x} + \frac{1}{\sin x} = \frac{\sin x + \cos x}{\sin x \cos x} $$
Thus, LHS = RHS.
- Proof for part (d)
Starting with:
$$ \text{LHS} = \tan^2 \beta + \cos^2 \beta + \sin^2 \beta $$
Use the identity $\sin^2 \beta + \cos^2 \beta = 1$:
$$ \text{LHS} = \tan^2 \beta + 1 $$
Since $\tan^2 \beta = \frac{\sin^2 \beta}{\cos^2 \beta}$, thus:
$$ \text{LHS} = \frac{\sin^2 \beta + \cos^2 \beta}{\cos^2 \beta} = \frac{1}{\cos^2 \beta} $$
Confirm $\text{LHS} = \text{RHS}$.
- Proof for part (e)
Start with:
$$ \text{LHS} = \sin\left(\frac{\pi}{4} + x\right) + \sin\left(\frac{\pi}{4} - x\right) $$
Using the sine addition formula gives:
$$ \text{LHS} = \sqrt{2} \left( \cos x + \sin x \right) $$
This matches the right-hand side:
$$ \text{RHS} = \sqrt{2} \cos x + \sqrt{2} \sin x $$
Thus, $\text{LHS} = \text{RHS}$.
- Proof for part (f)
Starting with the left-hand side:
$$ \text{LHS} = \sin\left(\frac{\pi}{2} - x\right) \cot\left(\frac{\pi}{2} + x\right) $$
Using the identities: $\sin\left(\frac{\pi}{2} - x\right) = \cos x$ and $\cot\left(\frac{\pi}{2} + x\right) = -\tan x$, we find:
$$ \text{LHS} = \cos x \cdot (-\tan x) = -\frac{\sin x}{\cos x} \cdot \cos x = -\sin x $$
Thus, $\text{LHS} = \text{RHS}$.
a) $\cos x \tan^3 x = \sin x \tan^2 x$
b) $\sin^2 \theta + \cos^4 \theta = \cos^2 \theta + \sin^4 \theta$
c) $(\sin x + \cos x) \frac{\tan^2 x + 1}{\tan x} = \frac{1}{\cos x} + \frac{1}{\sin x}$
d) $\tan^2 \beta + \cos^2 \beta + \sin^2 \beta = \frac{1}{\cos^2 \beta}$
e) $\sin\left(\frac{\pi}{4} + x\right) + \sin\left(\frac{\pi}{4} - x\right) = \sqrt{2}\cos x + \sqrt{2}\sin x$
f) $\sin\left(\frac{\pi}{2} - x\right) \cot\left(\frac{\pi}{2} + x\right) = -\sin x$
More Information
Trigonometric identities are useful in simplifying expressions or proving equalities. This problem applies various identities such as the Pythagorean identity, sine, cosine, and tangent definitions, along with angle addition and subtraction formulas.
Tips
- Forgetting to apply fundamental identities like $\sin^2 x + \cos^2 x = 1$ can lead to errors.
- Not simplifying expressions properly during manipulation can cloud the proof.
- Confusing sine and cosine values for angle variations.
AI-generated content may contain errors. Please verify critical information