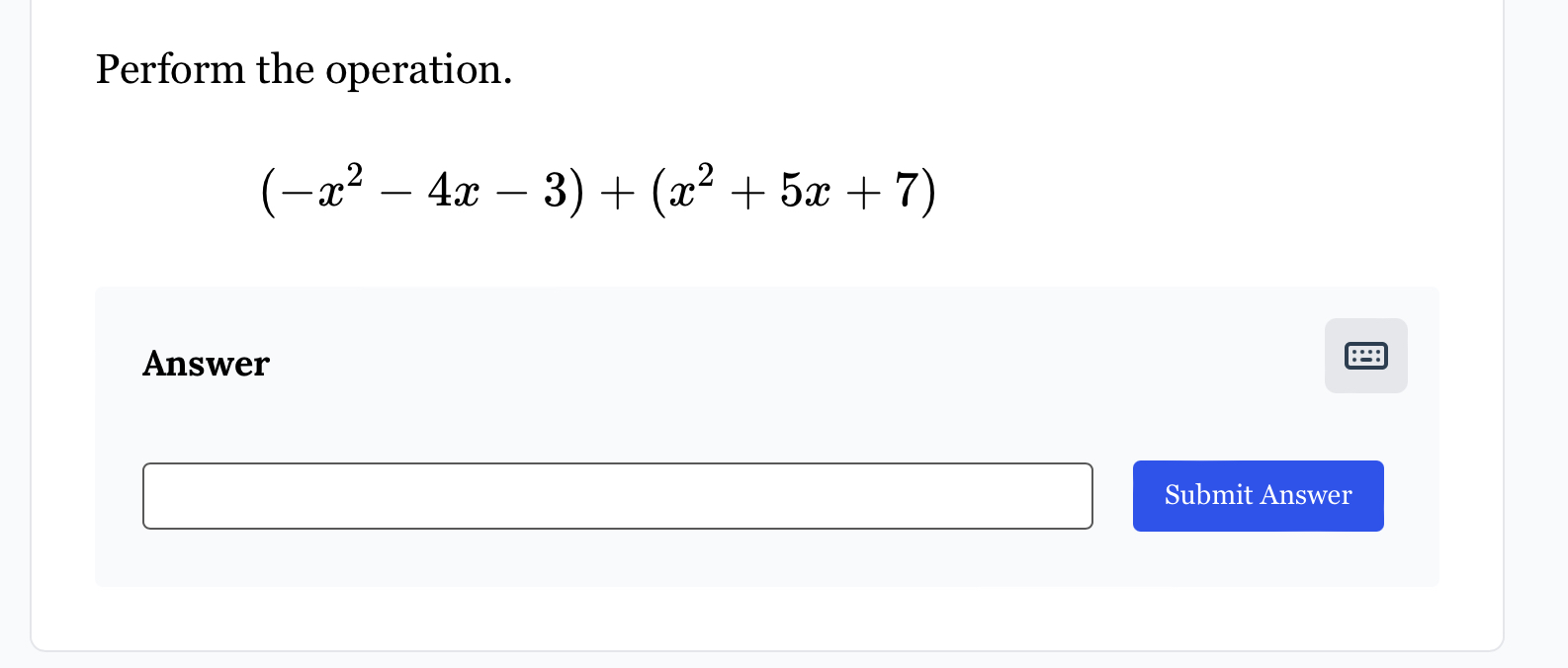
Perform the operation. (-x^2 - 4x - 3) + (x^2 + 5x + 7)
Understand the Problem
The question asks us to perform the operation of adding two polynomials together. Specifically, we need to combine the terms from both expressions to produce a single polynomial.
Answer
The result is $x + 4$.
Answer for screen readers
The final result of the operation is $x + 4$.
Steps to Solve
- Write down both polynomials
We have the two polynomials:
$P_1 = -x^2 - 4x - 3$
$P_2 = x^2 + 5x + 7$
- Combine like terms
Next, we will add the corresponding terms from each polynomial:
- For $x^2$ terms: $-x^2 + x^2$
- For $x$ terms: $-4x + 5x$
- For constant terms: $-3 + 7$
- Perform the additions for each term
Now, let's calculate each combination:
- $-x^2 + x^2 = 0$
- $-4x + 5x = 1x$ or simply $x$
- $-3 + 7 = 4$
- Write the final polynomial
Combine the results from the previous step:
$$P_{final} = 0 + 1x + 4$$
This simplifies to $x + 4$.
The final result of the operation is $x + 4$.
More Information
When adding polynomials, you simply combine like terms, ensuring that you only add coefficients of the same degree. In this case, the highest degree terms canceled out.
Tips
- Forgetting to combine all like terms (mainly coefficients).
- Miscalculating the signs when adding terms, especially when dealing with negative coefficients.
AI-generated content may contain errors. Please verify critical information