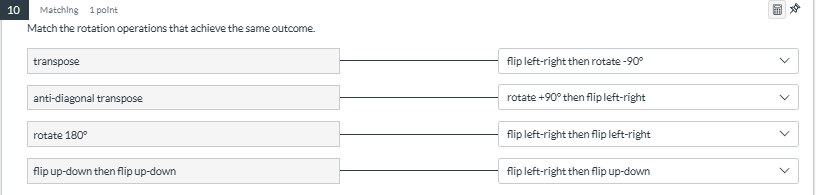
Match the rotation operations that achieve the same outcome: transpose, anti-diagonal transpose, rotate 180°, flip up-down then flip up-down.
Understand the Problem
The question is asking to match different rotation operations with their equivalent outcomes. This requires an understanding of matrix transformations and how different operations affect the position of elements within a matrix.
Answer
- Transpose: flip left-right then rotate -90° - Anti-diagonal transpose: rotate +90° then flip left-right - Rotate 180°: flip left-right then flip up-down - Flip up-down: flip left-right then flip up-down
Answer for screen readers
- Transpose: flip left-right then rotate -90°
- Anti-diagonal transpose: rotate +90° then flip left-right
- Rotate 180°: flip left-right then flip up-down
- Flip up-down: flip left-right then flip up-down
Steps to Solve
-
Identifying Matrix Operations
Understanding what each operation does to a matrix is crucial.- Transpose: Flips the matrix over its diagonal.
- Anti-diagonal Transpose: Flips the matrix over its anti-diagonal.
- Rotate 180°: Rotates the matrix by 180 degrees.
- Flip left-right: Mirrors the matrix along the vertical axis.
- Flip up-down: Mirrors the matrix along the horizontal axis.
-
Matching Transpose
The transpose operation can be matched with flip left-right then rotate -90°.- Transposing a matrix and then flipping it horizontally will yield the same result as performing a transpose directly.
-
Matching Anti-diagonal Transpose
The anti-diagonal transpose operation can be matched with rotate +90° then flip left-right.- Rotating the matrix +90° and then flipping left-right simulates the effect of an anti-diagonal transpose.
-
Matching Rotate 180°
The rotate 180° operation can be matched with flip left-right then flip up-down.- Flipping left-right and then flipping up-down achieves the same orientation as rotating the matrix 180°.
-
Matching Flip Up-Down
The flip up-down operation should be matched with flip left-right then flip up-down.- This operation changes the orientation in two axes, yielding the same effect as a direct flip up-down.
- Transpose: flip left-right then rotate -90°
- Anti-diagonal transpose: rotate +90° then flip left-right
- Rotate 180°: flip left-right then flip up-down
- Flip up-down: flip left-right then flip up-down
More Information
Matrix transformations play a significant role in areas such as computer graphics, image processing, and data transformations in machine learning. Understanding the relationships between different operations can enhance your analytical skills when working with matrices.
Tips
- Confusing transposition with simple flips. Transpose changes the positions of elements based on a specific diagonal.
- Misunderstanding the rotation directions. Remember that clockwise and counterclockwise rotations have different outcomes.
- Not visualizing the matrix before and after operations. Visual representation can clarify how each operation affects the matrix.
AI-generated content may contain errors. Please verify critical information