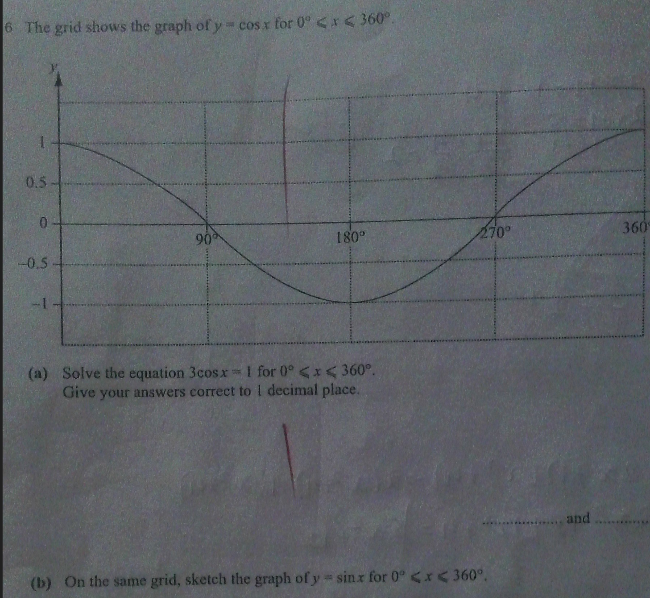
a) Solve the equation $3\cos x = 1$ for $0^{\circ} \le x \le 360^{\circ}$. Give your answers correct to 1 decimal place. b) On the same grid, sketch the graph of $y = \sin x$ for $... a) Solve the equation $3\cos x = 1$ for $0^{\circ} \le x \le 360^{\circ}$. Give your answers correct to 1 decimal place. b) On the same grid, sketch the graph of $y = \sin x$ for $0^{\circ} \le x \le 360^{\circ}$.
Understand the Problem
The question has two parts: (a) asks you to solve the trigonometric equation $3\cos x = 1$ for $0^{\circ} \le x \le 360^{\circ}$. You should give your answer correct to 1 decimal place, potentially using the provided graph of $y = \cos x$. (b) asks you to sketch the graph of $y = \sin x$ for $0^{\circ} \le x \le 360^{\circ}$ on the same grid.
Answer
(a) $x = 70.5^{\circ}$, $x = 289.5^{\circ}$ (b) Sketch of $y = \sin x$ for $0^{\circ} \le x \le 360^{\circ}$.
Answer for screen readers
(a) $x = 70.5^{\circ}$ and $x = 289.5^{\circ}$ (b) See the graph with the solution. Note that I cannot draw on the image directly, so you will have to use the description to complete the graph.
Steps to Solve
- Solve for $\cos x$
To isolate $\cos x$, divide both sides of the equation $3 \cos x = 1$ by 3: $$ \cos x = \frac{1}{3} $$
- Find the principal value of $x$
Use the inverse cosine function (arccos or $\cos^{-1}$) to find the principal value of $x$:
$$ x = \cos^{-1}\left(\frac{1}{3}\right) $$
Using a calculator, we find: $$ x \approx 70.5^{\circ} $$ This is the solution in the first quadrant.
- Find the second solution for $x$ within the given range
Since cosine is positive in the first and fourth quadrants, we need to find the angle in the fourth quadrant that has the same cosine value. We can find this angle by subtracting the principal value from $360^{\circ}$:
$$ x = 360^{\circ} - 70.5^{\circ} \approx 289.5^{\circ} $$
Therefore, the two solutions for $x$ in the range $0^{\circ} \le x \le 360^{\circ}$ are approximately $70.5^{\circ}$ and $289.5^{\circ}$.
- Sketch the graph of $y=\sin x$
Sketch the graph of $y = \sin x$ on the same grid as the graph of $y = \cos x$. The sine function starts at 0 at $0^\circ$, reaches its maximum value of 1 at $90^\circ$, returns to 0 at $180^\circ$, reaches its minimum value of -1 at $270^\circ$, and returns to 0 at $360^\circ$.
(a) $x = 70.5^{\circ}$ and $x = 289.5^{\circ}$ (b) See the graph with the solution. Note that I cannot draw on the image directly, so you will have to use the description to complete the graph.
More Information
The cosine function is positive in the first and fourth quadrants, which is why we have two solutions in the range $0^{\circ} \le x \le 360^{\circ}$. The sine function is positive in the first and second quadrants, and negative in the third and fourth quadrants. It has a maximum value of 1 and a minimum value of -1.
Tips
A common mistake is to only find the principal value and forget to find the other solution within the given range. Also, some students may have trouble sketching the sine graph particularly the placement of maximums and minimums.
AI-generated content may contain errors. Please verify critical information