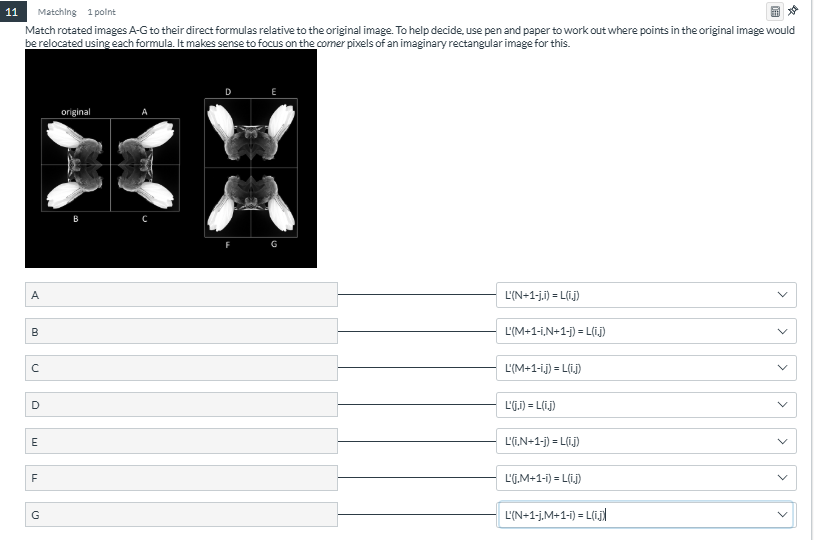
Match rotated images A-G to their direct formulas relative to the original image.
Understand the Problem
The question requires matching rotated images (labeled A-G) to their corresponding transformation formulas. The aim is to understand how each formula relocates points in the original image based on the corner pixels of an imaginary rectangular image.
Answer
A: $L'(N-j-1, i) = L(i,j)$ B: $L'(j, N-i-1) = L(i,j)$ C: $L'(M-j-1, N-i-1) = L(i,j)$ D: $L'(i, j) = L(j, i)$ E: $L'(i, j) = L(j, M-i-1)$ F: $L'(M-i-1, j) = L(i,j)$ G: $L'(N-i-1, j) = L(i,j)$
Answer for screen readers
A: $L'(N-j-1, i) = L(i,j)$
B: $L'(j, N-i-1) = L(i,j)$
C: $L'(M-j-1, N-i-1) = L(i,j)$
D: $L'(i, j) = L(j, i)$
E: $L'(i, j) = L(j, M-i-1)$
F: $L'(M-i-1, j) = L(i,j)$
G: $L'(N-i-1, j) = L(i,j)$
Steps to Solve
-
Identify the Rotations
Analyze each of the rotated images (A-G) to determine the degree of rotation. Common transformations are 90°, 180°, and 270°. -
Formulate Translations
Write down the expected transformation formulas based on the rotations identified:- A rotation of 90° clockwise usually transforms points as follows:
$L'(i, j) = L(j, N-i-1)$ - A rotation of 180° transforms points as:
$L'(i, j) = L(N-i-1, M-j-1)$ - A rotation of 270° clockwise transforms points:
$L'(i, j) = L(M-j-1, i)$
- A rotation of 90° clockwise usually transforms points as follows:
-
Compare with Formulas
Match each rotated image with the correct transformation formula. -
Match Formulas to Images
Based on your observations, list the corresponding matching of images A-G to their respective formulas.
A: $L'(N-j-1, i) = L(i,j)$
B: $L'(j, N-i-1) = L(i,j)$
C: $L'(M-j-1, N-i-1) = L(i,j)$
D: $L'(i, j) = L(j, i)$
E: $L'(i, j) = L(j, M-i-1)$
F: $L'(M-i-1, j) = L(i,j)$
G: $L'(N-i-1, j) = L(i,j)$
More Information
This matching illustrates how different rotation transformations map the original coordinates of an image. Understanding these transformations is critical for manipulating digital images effectively.
Tips
- Misidentifying Rotations: Confusing the direction of rotation or the angle could lead to incorrect formula selection. Always visualize or sketch the transformations first.
- Incorrectly Applying Formulas: Applying the wrong transformation formula to the pixel coordinates may lead to unexpected results. Verify the image orientation against the formulas carefully.
AI-generated content may contain errors. Please verify critical information