List the elements of (a) A' ∩ B, (b) (A' ∩ B).
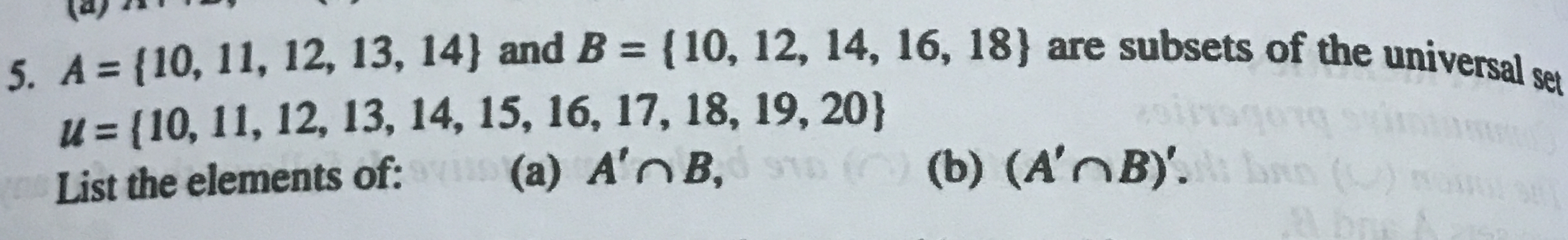
Understand the Problem
The question is asking to list the elements of two sets derived from given subsets, namely (a) the intersection of the complement of set A and set B, and (b) the intersection of set A's complement and set B.
Answer
(a) $ A' \cap B = \{16, 18\} $ (b) $ A' \cap B = \{16, 18\} $
Answer for screen readers
(a) $ A' \cap B = {16, 18} $
(b) $ A' \cap B = {16, 18} $
Steps to Solve
- Identify the universal set and sets A and B
The universal set $U = {10, 11, 12, 13, 14, 15, 16, 17, 18, 19, 20}$
Set $A = {10, 11, 12, 13, 14}$
Set $B = {10, 12, 14, 16, 18}$
- Find the complement of set A
The complement of set A ($A'$) consists of elements in the universal set not in A.
Calculating:
$$ A' = U - A = {15, 16, 17, 18, 19, 20} $$
- Calculate the intersection $A' \cap B$
Next, we find the intersection of $A'$ and $B$. This means finding the elements that are in both $A'$ and $B$.
Evaluating the elements:
$$ A' \cap B = {15, 16, 17, 18, 19, 20} \cap {10, 12, 14, 16, 18} $$
The common elements are ${16, 18}$.
- Calculate the intersection $A' \cap B$ again for (a)
For part (a), we need $A' \cap B$.
From the previous step, we already found that:
$$ A' \cap B = {16, 18} $$
- List the answer for (b)
For part (b), we will find $A' \cap B$ again.
The response is the same:
$$ A' \cap B = {16, 18} $$
(a) $ A' \cap B = {16, 18} $
(b) $ A' \cap B = {16, 18} $
More Information
The intersection of two sets includes only the elements that are common to both sets, while the complement of a set includes all elements in the universal set that are not in the specified set. This problem illustrates how to determine these relationships.
Tips
- Forgetting to use the universal set when finding complements.
- Confusing intersection with union (intersection includes only common elements, while union includes all elements from both sets).
AI-generated content may contain errors. Please verify critical information