lim as z approaches 5 of ( (1/(z + 5)) / (z + 5) )
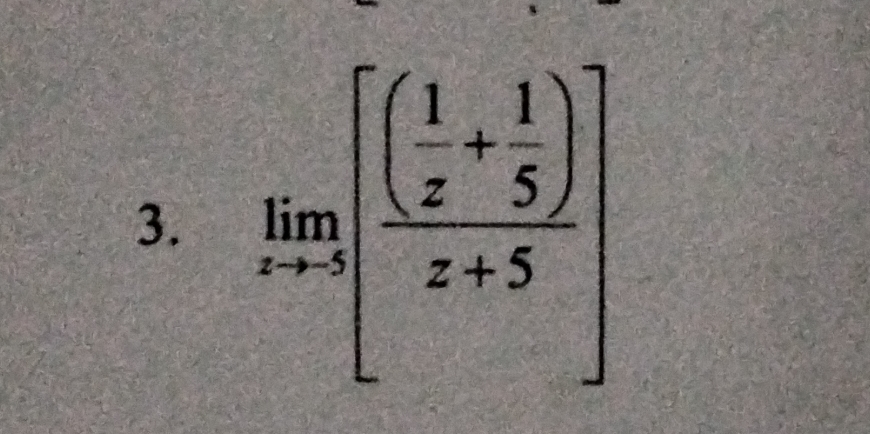
Understand the Problem
The question is asking to evaluate the limit of a complex expression as z approaches 5. This involves determining the behavior of the function around that point.
Answer
The limit is \( \frac{1}{25} \).
Answer for screen readers
The limit is ( \frac{1}{25} ).
Steps to Solve
-
Identify the limit expression We want to evaluate the limit as ( z ) approaches 5 for the expression:
$$ \lim_{z \to 5} \frac{\frac{1}{z} + \frac{1}{5}}{z + 5} $$ -
Substitute the value of z Substituting ( z = 5 ) into the expression gives us:
$$ \frac{\frac{1}{5} + \frac{1}{5}}{5 + 5} $$ -
Simplify the expression Calculating the numerator and the denominator:
The numerator becomes:
$$ \frac{1}{5} + \frac{1}{5} = \frac{2}{5} $$
The denominator becomes:
$$ 5 + 5 = 10 $$
Now the expression is:
$$ \frac{\frac{2}{5}}{10} $$
- Final calculation
Now calculate the final limit:
$$ \frac{\frac{2}{5}}{10} = \frac{2}{5} \cdot \frac{1}{10} = \frac{2}{50} = \frac{1}{25} $$
The limit is ( \frac{1}{25} ).
More Information
This limit involves evaluating a rational function by applying the concept of substitution directly after ensuring that the expression is defined at the limit point.
Tips
- Forgetting to simplify: Many students jump straight to substituting without simplifying the expression first.
- Dividing by zero: Always check that the denominator does not equal zero before substituting.
AI-generated content may contain errors. Please verify critical information