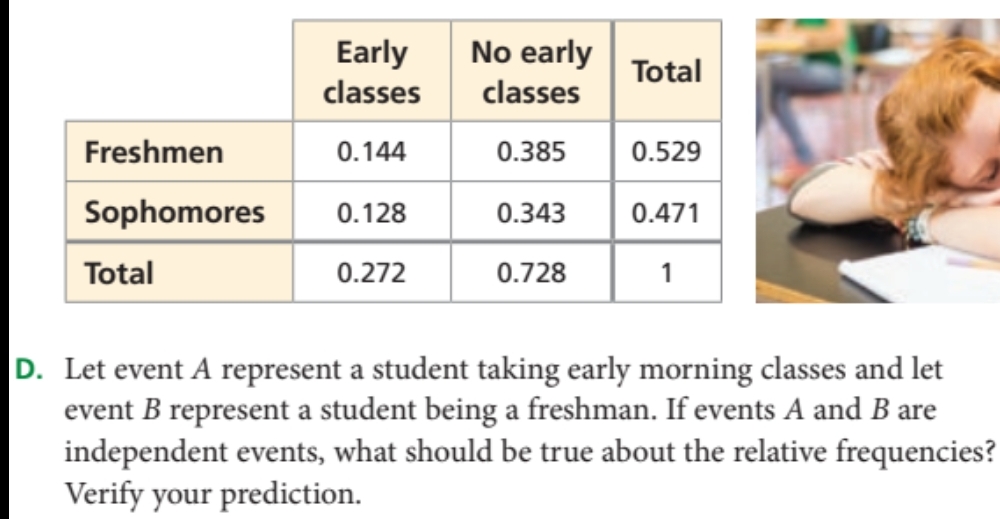
Let event A represent a student taking early morning classes and let event B represent a student being a freshman. If events A and B are independent events, what should be true abo... Let event A represent a student taking early morning classes and let event B represent a student being a freshman. If events A and B are independent events, what should be true about the relative frequencies? Verify your prediction.
Understand the Problem
The question asks what should be true about the relative frequencies if two events, A (taking early morning classes) and B (being a freshman), are independent. The user is required to verify their prediction based on the provided data.
Answer
A and B are not independent events.
Answer for screen readers
Events A (taking early morning classes) and B (being a freshman) are not independent.
Steps to Solve
-
Understand Independence of Events For two events, A and B, to be independent, it must hold true that: $$ P(A \cap B) = P(A) \cdot P(B) $$ This means the probability of both A and B occurring together should equal the product of their individual probabilities.
-
Identify the Probabilities From the table:
- For Early Classes (A):
- $P(A) = P(A \text{ and Freshman}) + P(A \text{ and Sophomore}) = 0.144 + 0.128 = 0.272$
- For Freshmen (B):
- $P(B) = 0.144$
-
Calculate Joint Probability of A and B The joint probability of A and B can be expressed as $P(A \cap B) = 0.144$ since this corresponds to freshmen taking early classes.
-
Check Independence Condition Now verify if: $$ P(A \cap B) = P(A) \cdot P(B) $$ By substituting the values: $$ 0.144 \stackrel{?}{=} 0.272 \cdot 0.144 $$
-
Perform the Calculation Calculate: $$ 0.272 \cdot 0.144 = 0.039168 $$
-
Compare the Results Now compare $0.144$ with $0.039168$. Since they are not equal, we conclude that A and B are not independent.
Events A (taking early morning classes) and B (being a freshman) are not independent.
More Information
This conclusion indicates that the likelihood of being a freshman and taking early morning classes is not simply a function of their individual probabilities. Their relationship suggests some form of dependence.
Tips
- Misinterpreting Independence: A common mistake is assuming that because the probabilities are non-zero, the events must be independent. Always check the independence condition mathematically.
- Forgetting to Calculate Joint Probability: Skipping the calculation of the joint probability can lead to incorrect conclusions about independence.
AI-generated content may contain errors. Please verify critical information