Let a̅ = -i - j + k, a̅.b̅ = 1 and a̅ × b̅ = i - j. Then a̅ - 6b̅ is equal to:
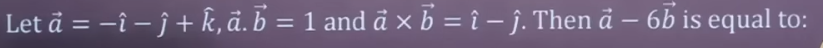
Understand the Problem
The question is asking for the evaluation of the expression a̅ - 6b̅ given the vectors a̅ and b̅ and their properties. We need to substitute the known values and perform the necessary calculations to find the result.
Answer
$$ \mathbf{a} - 6\mathbf{b} = -5\mathbf{i} + 7\mathbf{j} - \mathbf{k} $$
Answer for screen readers
$$ \mathbf{a} - 6\mathbf{b} = -5\mathbf{i} + 7\mathbf{j} - \mathbf{k} $$
Steps to Solve
- Identify the given vectors and properties
The problem gives the vector
$$ \mathbf{a} = -\mathbf{i} - \mathbf{j} + \mathbf{k} $$
along with the inner product and cross product:
$$ \mathbf{a} \cdot \mathbf{b} = 1 $$
$$ \mathbf{a} \times \mathbf{b} = \mathbf{i} - \mathbf{j} $$
- Find the expression for $\mathbf{b}$
From the cross product, we can infer some properties about $\mathbf{b}$.
Let $$ \mathbf{b} = x\mathbf{i} + y\mathbf{j} + z\mathbf{k} $$.
Using the property of the dot product:
$$ \mathbf{a} \cdot \mathbf{b} = (-1)(x) + (-1)(y) + (1)(z) = -x - y + z = 1 $$
This gives us our first equation:
$$ z - x - y = 1 \quad \text{(1)} $$
- Use the cross product to find another equation
The cross product is computed as follows:
$$ \mathbf{a} \times \mathbf{b} = \begin{vmatrix}
\mathbf{i} & \mathbf{j} & \mathbf{k} \
-1 & -1 & 1 \
x & y & z
\end{vmatrix} $$
Calculating the determinant, we find that:
$$ \mathbf{a} \times \mathbf{b} = \left((-1)z - (1)(y)\right)\mathbf{i} - \left((-1)z - (1)(x)\right)\mathbf{j} + \left((-1)(y) - (-1)(x)\right)\mathbf{k} $$
That simplifies to:
$$ = (-z - y)\mathbf{i} - (-z - x)\mathbf{j} + (x - y)\mathbf{k} $$
We know this should equal:
$$ \mathbf{i} - \mathbf{j} $$
This gives us two additional equations:
-
$-z - y = 1 \quad \text{(2)}$
-
$z + x = 1 \quad \text{(3)}$
-
Solve the system of equations
We now have three equations:
- ( z - x - y = 1 ) (from step 2)
- ( -z - y = 1 ) (from step 3)
- ( z + x = 1 ) (from step 3)
From equation (2):
$$ y = -z - 1 $$
Substituting ( y ) from equation (2) into equation (1) gives:
$$ z - x - (-z - 1) = 1 $$
Which simplifies to:
$$ 2z - x + 1 = 1 \implies x = 2z $$
Substituting ( x ) back into equation (3):
$$ z + 2z = 1 \implies 3z = 1 \implies z = \frac{1}{3} $$
Now substituting ( z ) back to find ( x ) and ( y ):
$$ x = 2 \cdot \frac{1}{3} = \frac{2}{3} $$
$$ y = -\frac{1}{3} - 1 = -\frac{4}{3} $$
Thus, we find
$$ \mathbf{b} = \frac{2}{3} \mathbf{i} - \frac{4}{3} \mathbf{j} + \frac{1}{3} \mathbf{k} $$
- Substituting in the expression $\mathbf{a} - 6\mathbf{b}$
Now substitute ( \mathbf{b} ) back into the original expression:
$$ \mathbf{a} - 6\mathbf{b} = (-\mathbf{i} - \mathbf{j} + \mathbf{k}) - 6\left(\frac{2}{3} \mathbf{i} - \frac{4}{3} \mathbf{j} + \frac{1}{3} \mathbf{k}\right) $$
Distributing gives:
$$ = -\mathbf{i} - \mathbf{j} + \mathbf{k} - 4\mathbf{i} + 8\mathbf{j} - 2\mathbf{k} $$
Combine like terms:
$$ = (-1 - 4)\mathbf{i} + (-1 + 8)\mathbf{j} + (1 - 2)\mathbf{k} $$
$$ = -5\mathbf{i} + 7\mathbf{j} - \mathbf{k} $$
$$ \mathbf{a} - 6\mathbf{b} = -5\mathbf{i} + 7\mathbf{j} - \mathbf{k} $$
More Information
The answer shows how vector subtraction and scalar multiplication affect the components of vectors. In vector algebra, operations like these are commonly used in physics and engineering.
Tips
- Miscalculating the cross product: It's crucial to compute the determinant correctly. Double-check each coefficient.
- Not substituting back correctly: Ensure all values are replaced properly in final calculations.
AI-generated content may contain errors. Please verify critical information