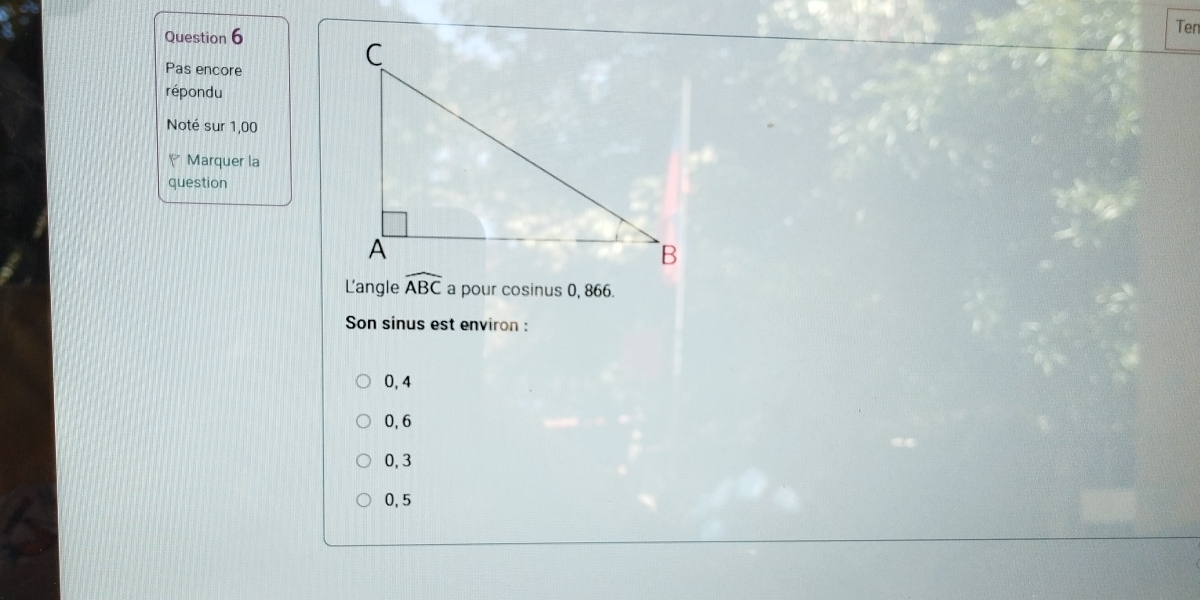
L'angle ABC a pour cosinus 0, 866. Son sinus est environ :
Understand the Problem
La question demande de calculer le sinus d'un angle dont le cosinus est donné comme 0,866. On cherche à trouver la valeur approximative du sinus à partir de cette information.
Answer
Le sinus est environ $0.5$.
Answer for screen readers
Le sinus de l'angle ABC est environ $0.5$.
Steps to Solve
-
Utiliser l'identité trigonométrique Pour calculer le sinus à partir du cosinus, nous utilisons l'identité suivante : $$ \sin^2(x) + \cos^2(x) = 1 $$ Ici, nous connaissons le cosinus : $ \cos(x) = 0.866 $.
-
Calculer le carré du cosinus Calculons le carré du cosinus : $$ \cos^2(x) = (0.866)^2 = 0.749956 $$
-
Isoler le sinus dans l'identité trigonométrique En réarrangeant l'identité, nous avons : $$ \sin^2(x) = 1 - \cos^2(x) $$ Substituons :
$$ \sin^2(x) = 1 - 0.749956 = 0.250044 $$
- Calculer le sinus Pour trouver le sinus, prenons la racine carrée de ce résultat : $$ \sin(x) = \sqrt{0.250044} \approx 0.5 $$
Le sinus de l'angle ABC est environ $0.5$.
More Information
Le sinus et le cosinus d'un angle sont liés par l'identité trigonométrique fondamentale. Dans cet exemple, nous avons utilisé cette relation pour trouver le sinus à partir du cosinus donné.
Tips
- Confondre le sinus et le cosinus lors des calculs.
- Oublier de prendre en compte le signe du sinus. Dans ce cas, pour un angle aigu, le sinus sera positif.
AI-generated content may contain errors. Please verify critical information