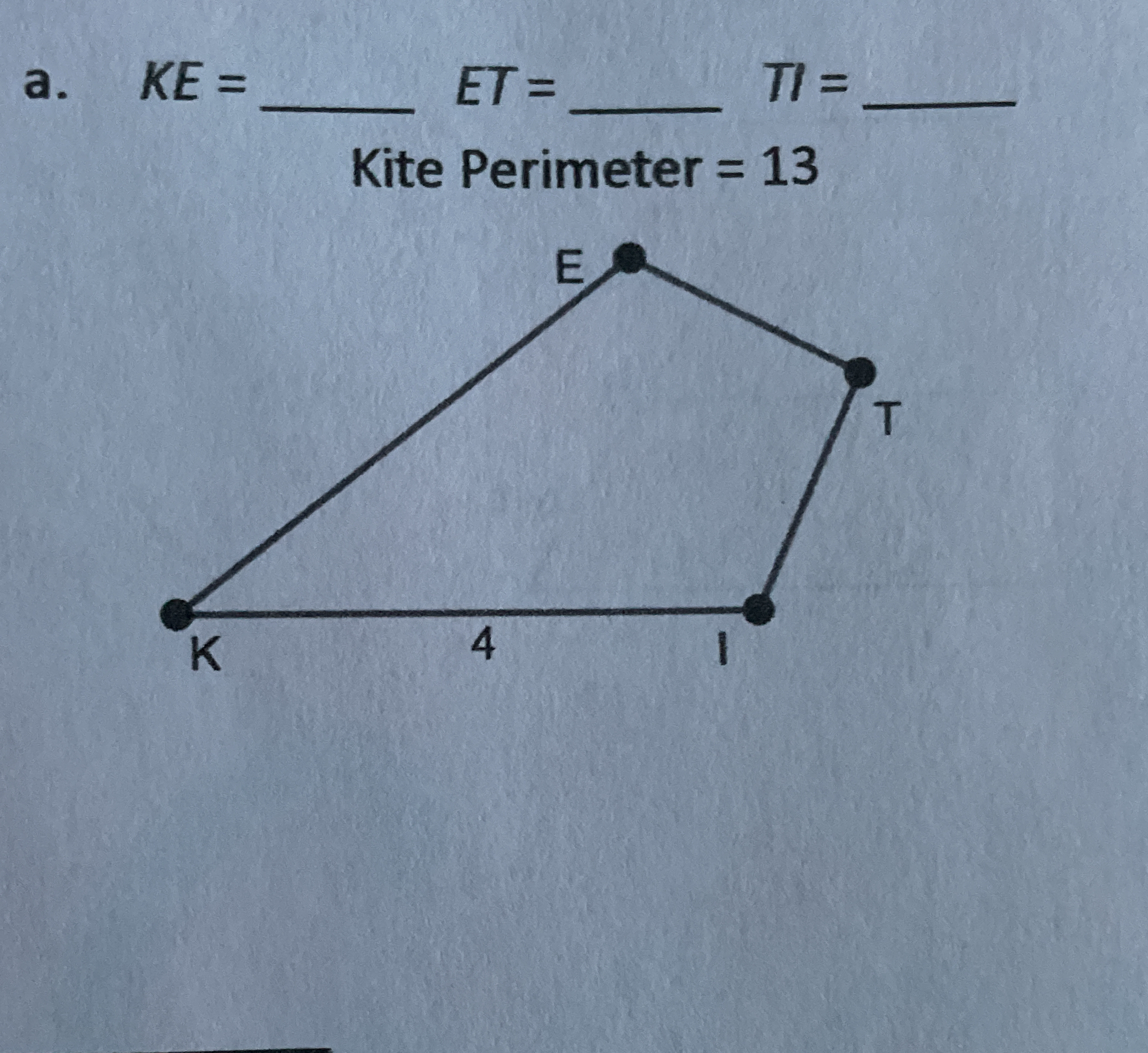
KE = _____ ET = _____ TI = _____ Kite Perimeter = 13
Understand the Problem
The question is asking us to find the lengths of the segments KE, ET, and TI in a kite with a given perimeter of 13. Since it is a kite, we can use the properties of kites, where two pairs of adjacent sides are equal, to solve for the unknown lengths.
Answer
$KE = 3$, $ET = 3$, $TI = 3$
Answer for screen readers
$KE = 3$, $ET = 3$, $TI = 3$
Steps to Solve
- Identify Known Values
The perimeter of the kite is given as 13. We also know one side length, $KI = 4$.
- Set Up the Equation for Perimeter
In a kite, the lengths of the sides are equal in pairs. We can denote the unknown lengths as $KE = ET = TI = x$.
The perimeter can be expressed as: $$ P = KE + ET + TI + KI = x + x + x + 4 $$
- Write the Perimeter Equation
Set up the equation using the perimeter value: $$ 3x + 4 = 13 $$
- Solve for x
Subtract 4 from both sides to isolate the terms with $x$: $$ 3x = 13 - 4 $$
Then simplify: $$ 3x = 9 $$
Now divide by 3: $$ x = \frac{9}{3} = 3 $$
- Determine the Lengths of Segments
Now we can determine the lengths of segments: $$ KE = ET = TI = 3 $$
$KE = 3$, $ET = 3$, $TI = 3$
More Information
The lengths of the segments in the kite are all equal to 3. This demonstrates the symmetry present in kite shapes where two pairs of adjacent sides are equal.
Tips
- Misunderstanding the properties of kites: Remember that in a kite, two pairs of adjacent sides are equal. If you forget this, you may set up the equation incorrectly.
- Incorrectly summing the perimeter: Ensure that you account for all sides when calculating perimeter.
AI-generated content may contain errors. Please verify critical information