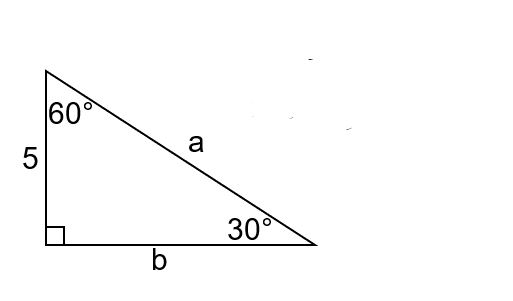
In the right triangle, find the lengths of sides a and b given that one side is 5 and the angles are 30° and 60°.
Understand the Problem
The question is asking to determine the lengths of sides 'a' and 'b' in a right triangle using trigonometric relationships, based on the given angle measures and one side's length.
Answer
The lengths of the sides are \( a = \frac{5\sqrt{3}}{2} \) and \( b = \frac{5\sqrt{3}}{2} \).
Answer for screen readers
The lengths of the sides are:
- ( a = \frac{5\sqrt{3}}{2} )
- ( b = \frac{5\sqrt{3}}{2} )
Steps to Solve
- Identify known values and angles
From the triangle, we know:
- Angle ( C = 60^\circ )
- Angle ( A = 30^\circ )
- Side ( c = 5 ) (the side opposite the right angle)
- Use the sine function to find side 'a'
For angle ( C ):
$$ \sin(60^\circ) = \frac{a}{c} $$
Substituting the known value for ( c ):
$$ \sin(60^\circ) = \frac{a}{5} $$
Now, we solve for ( a ):
$$ a = 5 \cdot \sin(60^\circ) $$
Using ( \sin(60^\circ) = \frac{\sqrt{3}}{2} ):
$$ a = 5 \cdot \frac{\sqrt{3}}{2} = \frac{5\sqrt{3}}{2} $$
- Use the cosine function to find side 'b'
For angle ( A ):
$$ \cos(30^\circ) = \frac{b}{c} $$
Substituting the known value for ( c ):
$$ \cos(30^\circ) = \frac{b}{5} $$
Now, we solve for ( b ):
$$ b = 5 \cdot \cos(30^\circ) $$
Using ( \cos(30^\circ) = \frac{\sqrt{3}}{2} ):
$$ b = 5 \cdot \frac{\sqrt{3}}{2} = \frac{5\sqrt{3}}{2} $$
The lengths of the sides are:
- ( a = \frac{5\sqrt{3}}{2} )
- ( b = \frac{5\sqrt{3}}{2} )
More Information
In a 30-60-90 triangle, the ratios of the sides are well-defined. The side opposite ( 30^\circ ) is ( x ), the side opposite ( 60^\circ ) is ( x\sqrt{3} ), and the hypotenuse is ( 2x ). Here, we substituted ( c = 5 ) to find the sides.
Tips
- Forgetting to use the correct angle functions (sine for opposite, cosine for adjacent).
- Mixing up the sides associated with each angle.
AI-generated content may contain errors. Please verify critical information