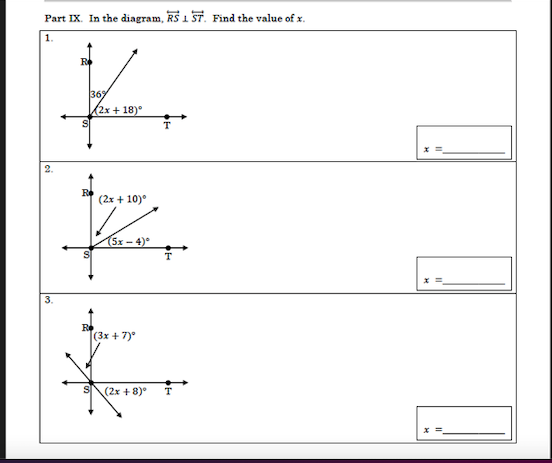
In the diagram, RS is parallel to ST. Find the value of x in the following equations: 1. 36° = (2x + 18)°, 2. (2x + 10)° = (5x - 4)°, 3. (3x + 7)° = (2x + 8)°.

Steps to Solve

1. Identify Relationships Between Angles

In each case, look for the relationship between the angles. Parallel lines cut by a transversal create angles that are either corresponding, alternate interior, or supplementary.

2. Set Up the Equation for Each Problem

Using the relationships identified, set up an equation for each part based on the angle measures provided.

For Part 1:

The angles ( 36^\circ ) and ( (2x + 18)^\circ ) are supplementary, so:

$$ 36 + (2x + 18) = 180 $$

For Part 2:

The angles ( (2x + 10)^\circ ) and ( (5x - 4)^\circ ) are corresponding, so:

$$ 2x + 10 = 5x - 4 $$

For Part 3:

The angles ( (3x + 7)^\circ ) and ( (2x + 8)^\circ ) are supplementary, so:

$$ (3x + 7) + (2x + 8) = 180 $$

3. Solve Each Equation

Now, solve for ( x ) in each case.

Part 1:

1. Rearranging the equation:

$$ 2x + 54 = 180 \implies 2x = 126 \implies x = 63 $$

Part 2:

1. Rearranging the equation:

$$ 2x + 10 = 5x - 4 \implies 10 + 4 = 5x - 2x \implies 14 = 3x \implies x = \frac{14}{3} \approx 4.67 $$

Part 3:

1. Rearranging the equation:

$$ 5x + 15 = 180 \implies 5x = 165 \implies x = 33 $$

4. Conclusion

Compute final values of ( x ) for each part based on the solution steps above.