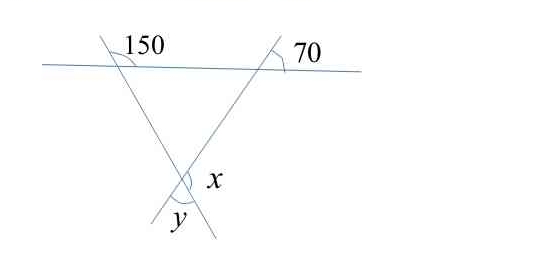
In the diagram, angle x and angle y need to be solved with respect to the given angles of 150 and 70 degrees.
Understand the Problem
The question is asking to find the values of angles x and y given the values of the angles around them. It relies on the properties of angles formed by intersecting lines, specifically the concept that angles on a straight line add up to 180 degrees.
Answer
The values of the angles are $x = 30^\circ$ and $y = 70^\circ$.
Answer for screen readers
The values of the angles are: $x = 30^\circ$ and $y = 70^\circ$.
Steps to Solve
- Identify angle relationships
From the diagram, we notice that angle 150° and angle $x$ are supplementary, meaning they add up to 180°.
- Set up the equation for $x$
Using the relationship that supplementary angles add up to 180°, we set up the equation: $$ 150 + x = 180 $$
- Solve for $x$
Subtract 150 from both sides to find the value of $x$: $$ x = 180 - 150 = 30 $$
- Identify angle $y$
Angle $y$ and angle 70° are vertically opposite angles, meaning they are equal: $$ y = 70 $$
- Summarize the results
We have now found both angles $x$ and $y$. The final values are:
- $x = 30$
- $y = 70$
The values of the angles are: $x = 30^\circ$ and $y = 70^\circ$.
More Information
The angles formed by intersecting lines create pairs of angles that can be supplementary or vertically opposite. This problem illustrates the importance of understanding these relationships to solve for unknown angles.
Tips
- Misinterpreting the relationships between angles; make sure to identify whether they are supplementary or vertically opposite.
- Forgetting to set up the equations correctly. Ensure you're applying the correct property for the angles involved.
AI-generated content may contain errors. Please verify critical information