In the diagram above QRTS, QR: TS = 2:3 find the ratio of the area of triangle PQR to the area of the trapezium QRST.
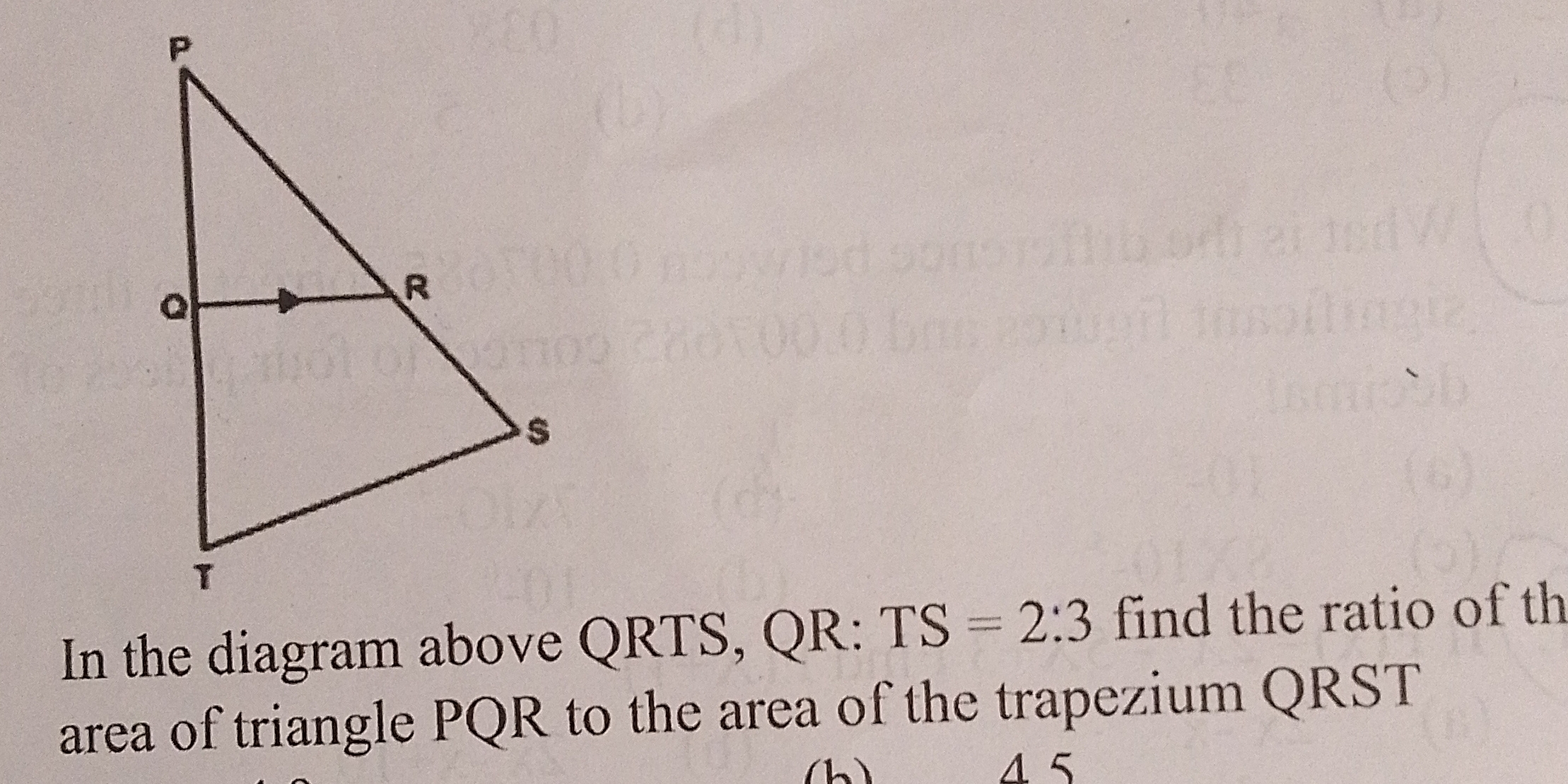
Understand the Problem
The question is asking to find the ratio of the area of triangle PQR to the area of the trapezium QRST, given the ratio of the segments QR and TS. This requires an understanding of geometric properties and area calculations.
Answer
The ratio is \( \frac{2}{5} \).
Answer for screen readers
The ratio of the area of triangle PQR to the area of trapezium QRST is ( \frac{2}{5} ).
Steps to Solve
-
Identify the segments and ratio The given ratio is ( QR:TS = 2:3 ). This means that if we denote ( QR = 2x ) and ( TS = 3x ), we can express the lengths in terms of a variable ( x ).
-
Calculate the area of triangle PQR The area of triangle PQR can be calculated using the formula: $$ \text{Area}{\triangle} = \frac{1}{2} \times \text{base} \times \text{height} $$ Here, ( QR ) is the base of the triangle and the height can be denoted by ( h ). Thus, $$ \text{Area}{\triangle PQR} = \frac{1}{2} \times QR \times h = \frac{1}{2} \times 2x \times h = xh $$
-
Calculate the area of trapezium QRST The area of trapezium QRST can be calculated using the formula: $$ \text{Area}{\text{trapezium}} = \frac{1}{2} \times (b_1 + b_2) \times h $$ where ( b_1 = QR = 2x ) and ( b_2 = TS = 3x ). Hence, $$ \text{Area}{QRST} = \frac{1}{2} \times (2x + 3x) \times h = \frac{1}{2} \times 5x \times h = \frac{5xh}{2} $$
-
Find the ratio of the areas Now we can find the ratio of the area of triangle PQR to the area of trapezium QRST: $$ \text{Ratio} = \frac{\text{Area}{\triangle PQR}}{\text{Area}{QRST}} = \frac{xh}{\frac{5xh}{2}} = \frac{xh \times 2}{5xh} = \frac{2}{5} $$
The ratio of the area of triangle PQR to the area of trapezium QRST is ( \frac{2}{5} ).
More Information
The area of a triangle and a trapezium can often be compared using the same height or base, depending on how they're oriented. Understanding these relationships helps in determining ratios effectively.
Tips
- Misinterpreting the segments and their ratios can lead to incorrect calculations. Ensure you assign the lengths correctly.
- Forgetting to simplify the ratios at the end can result in leaving the answer in an unhelpful form.
AI-generated content may contain errors. Please verify critical information