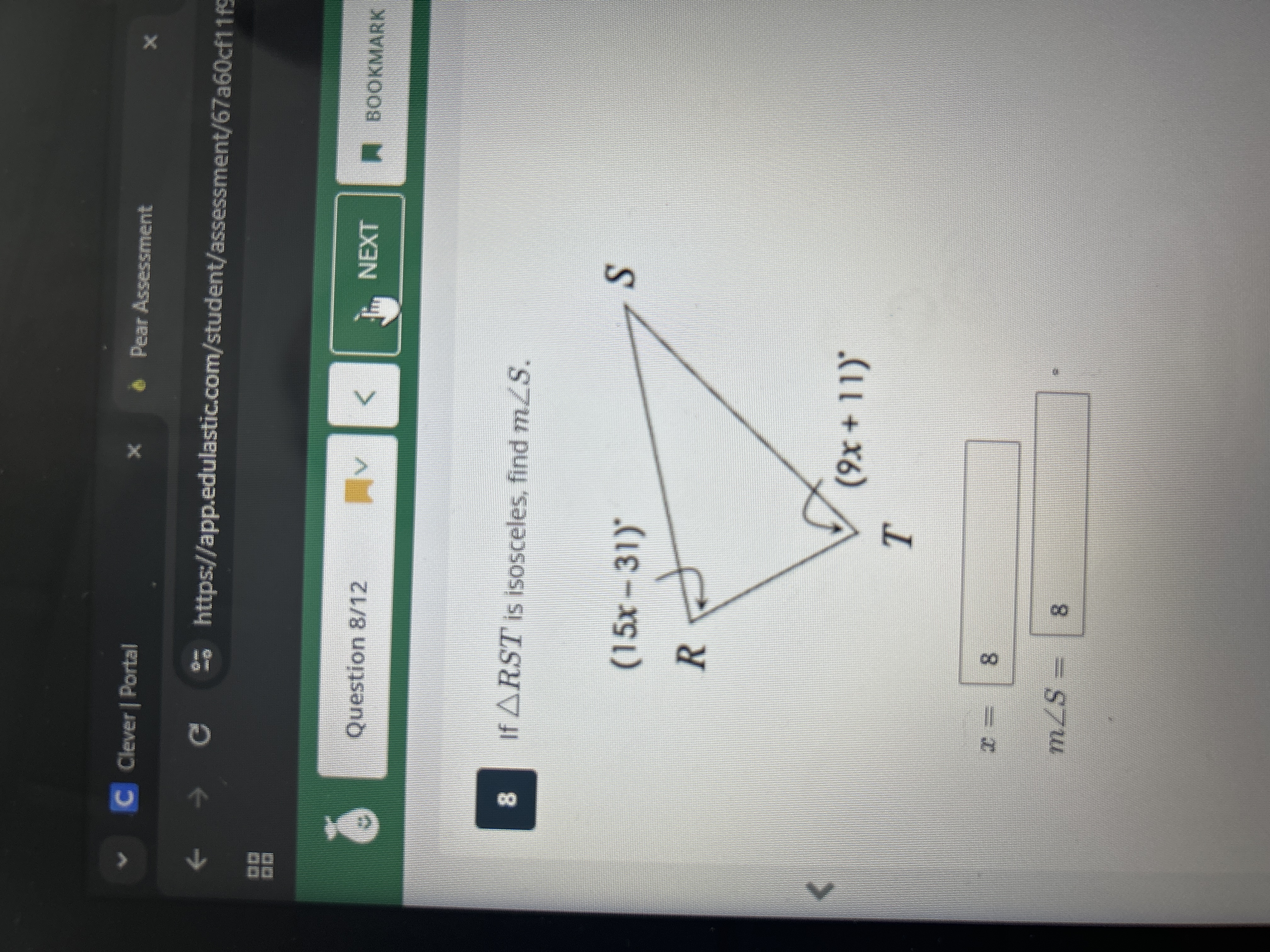
If triangle RST is isosceles, find the measure of angle S.
Understand the Problem
This is a geometry problem where we have an isosceles triangle RST, where angle R and angle T are equal in value. We are given expressions for angles R and T in terms of x and are asked to solve for x and then find the measure of angle S.
Answer
$x = 7$ $m\angle S = 32^{\circ}$
Answer for screen readers
$x = 7$ $m\angle S = 32^{\circ}$
Steps to Solve
-
Set up the equation Since $\triangle RST$ is isosceles and $\angle R$ and $\angle T$ are given, we can set them equal to each other to solve for $x$. This is because in an isosceles triangle, the angles opposite the equal sides are equal. $$15x - 31 = 9x + 11$$
-
Solve for $x$ Subtract $9x$ from both sides: $$15x - 9x - 31 = 9x - 9x + 11$$ $$6x - 31 = 11$$ Add 31 to both sides: $$6x - 31 + 31 = 11 + 31$$ $$6x = 42$$ Divide both sides by 6: $$\frac{6x}{6} = \frac{42}{6}$$ $$x = 7$$
-
Find the measure of $\angle R$ and $\angle T$ Substitute $x = 7$ into the expression for $\angle R$: $$\angle R = (15(7) - 31)^{\circ} = (105 - 31)^{\circ} = 74^{\circ}$$ Since $\angle R = \angle T$, then $\angle T = 74^{\circ}$.
-
Find the measure of $\angle S$ The sum of the angles in a triangle is $180^{\circ}$. Therefore: $$\angle R + \angle T + \angle S = 180^{\circ}$$ $$74^{\circ} + 74^{\circ} + \angle S = 180^{\circ}$$ $$148^{\circ} + \angle S = 180^{\circ}$$ Subtract $148^{\circ}$ from both sides: $$\angle S = 180^{\circ} - 148^{\circ}$$ $$\angle S = 32^{\circ}$$
$x = 7$ $m\angle S = 32^{\circ}$
More Information
The problem utilizes the properties of an isosceles triangle, where two sides are of equal length, and consequently, the angles opposite those sides are equal. It also uses the angle sum property of a triangle, which states that the sum of the interior angles of a triangle is always $180^{\circ}$.
Tips
A common mistake might be incorrectly setting up the equation or making an algebraic error when solving for $x$. Another mistake would be not using the value of $x$ to find the measure of angles $R$ and $T$ before calculating the measure of angle $S$. For example, assuming $x$ is the answer to the question's objective, to find the measure of angle $S$.
AI-generated content may contain errors. Please verify critical information