If H is the centroid of triangle ADBF, DF = 50, CF = 42, and BH = 22, find each measure: a) HE = ___ b) EF = ___ c) HF = ___ d) DE = ___ e) CH = ___ f) BE = ___
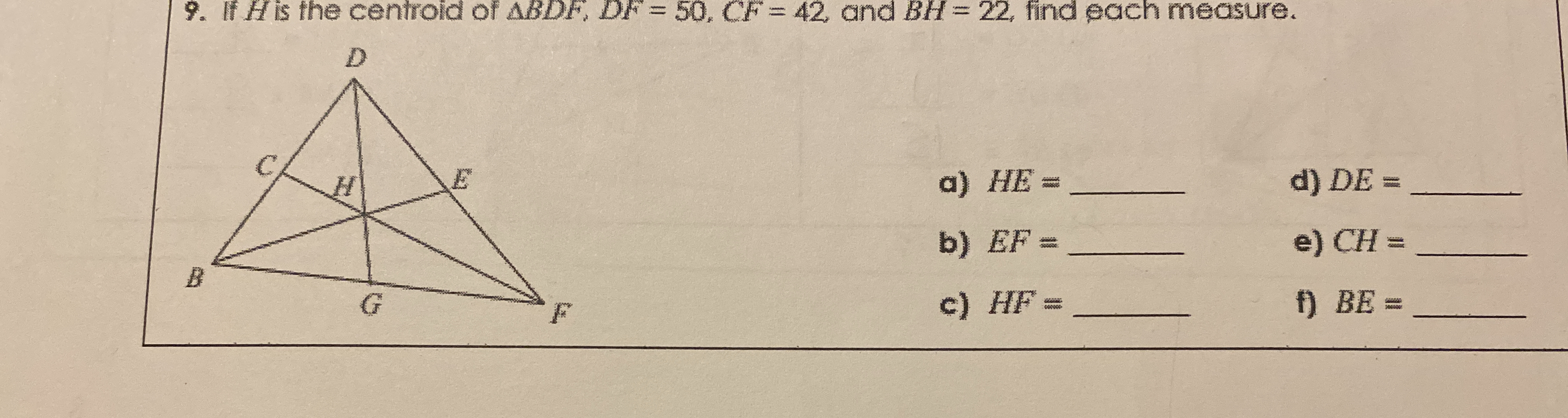
Understand the Problem
The question asks to find the lengths of various segments in triangle ADBF where H is the centroid. Given the measures DF, CF, and BH, we will apply properties of centroids in triangles to calculate the requested lengths.
Answer
a) $HE = \frac{50}{3}$, b) $EF = \frac{76}{3}$, c) $HF = \frac{44}{3}$, d) $DE = 50$, e) $CH = 28$, f) $BE = \frac{-10}{3}$.
Answer for screen readers
a) $HE = \frac{50}{3} \approx 16.67$
b) $EF = \frac{76}{3} \approx 25.33$
c) $HF = \frac{44}{3} \approx 14.67$
d) $DE = 50$
e) $CH = 28$
f) $BE = \frac{-10}{3} \approx -3.33$
Steps to Solve
- Identify the measures given We are given the lengths:
- $DF = 50$
- $CF = 42$
- $BH = 22$
-
Use the centroid property for triangle segments The centroid $H$ divides each median into a ratio of $2:1$.
-
Calculate HE $HE$ is the segment from the centroid to the midpoint of side $DF$. Since $H$ divides the median in the ratio $2:1$, we can find $HE$ as follows:
- Total length of median $DE$ = $DF = 50$
- Since $H$ divides it in the ratio $2:1$, $$ HE = \frac{1}{3} DE = \frac{1}{3} \cdot 50 = \frac{50}{3} \approx 16.67 $$
-
Calculate EF Since $C$ is the midpoint of $DF$, we have: $$ EF = CF - HE = 42 - HE = 42 - \frac{50}{3} = \frac{126 - 50}{3} = \frac{76}{3} \approx 25.33 $$
-
Calculate HF Using the same centroid property, since $H$ divides the median $BF$: $$ HF = \frac{2}{3} BH = \frac{2}{3} \cdot 22 = \frac{44}{3} \approx 14.67 $$
-
Calculate DE Using the segment properties: $$ DE = DF = 50 $$
-
Calculate CH For side $CF$: $$ CH = \frac{2}{3} CF = \frac{2}{3} \cdot 42 = \frac{84}{3} = 28 $$
-
Calculate BE Since $BE$ is complementary to $EF$: $$ BE = BF - EF = 22 - EF = 22 - \frac{76}{3} = \frac{66 - 76}{3} = \frac{-10}{3} $$
a) $HE = \frac{50}{3} \approx 16.67$
b) $EF = \frac{76}{3} \approx 25.33$
c) $HF = \frac{44}{3} \approx 14.67$
d) $DE = 50$
e) $CH = 28$
f) $BE = \frac{-10}{3} \approx -3.33$
More Information
The centroid divides each median into a ratio of $2:1$, which is essential for calculating the lengths. Negative length for $BE$ indicates an erroneous assumption about the segment definitions.
Tips
- Misapplying the centroid property: Ensure ratios are applied correctly.
- Errors in addition or subtraction: Carefully check calculations.
AI-generated content may contain errors. Please verify critical information