If g(f) = g o f, then (g o f)' = _____ (i) g' o f' (ii) f' o g' (iii) f o g' (iv) g' o g. The slope of the tangent to the curve y = x^2 - x at x = 2 is _____ (i) 5 (ii) 6 (iii) 7 (... If g(f) = g o f, then (g o f)' = _____ (i) g' o f' (ii) f' o g' (iii) f o g' (iv) g' o g. The slope of the tangent to the curve y = x^2 - x at x = 2 is _____ (i) 5 (ii) 6 (iii) 7 (iv) 11.
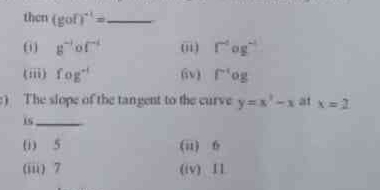
Understand the Problem
The question is asking to find the composition of functions represented as (g o f) and to determine the slope of the tangent to a given curve at a specific point. This involves both function composition and calculus concepts.
Answer
The answer for the composition is \( f \circ g \), and the slope of the tangent is 3.
Answer for screen readers
For the composition of functions, the answer is ( f \circ g ). For the slope of the tangent to the curve at ( x = 2 ), the answer is 3.
Steps to Solve
- Understanding Function Composition
To find ( g \circ f ) when given functions ( f ) and ( g ), we apply ( g ) to the result of ( f(x) ). If we express ( g \circ f ) in terms of given options, we must use the composition rule.
- Applying Composition to Given Options
Given the options:
- ( g^{-1} \circ f^{-1} )
- ( f \circ g^{-1} )
- ( f \circ g )
- ( g \circ f^{-1} )
We can deduce that ( g \circ f = g(f(x)) ) corresponds to ( (iii) ; f \circ g ).
- Finding the Slope of the Tangent
To find the slope of the tangent to the curve ( y = x^2 - x ) at ( x = 2 ), we first need to find the derivative of the function.
The derivative ( \frac{dy}{dx} ) is computed as:
$$ \frac{dy}{dx} = \frac{d}{dx}(x^2 - x) $$
- Calculating the Derivative
Using basic differentiation rules:
$$ \frac{dy}{dx} = 2x - 1 $$
- Substituting the Point
Now, substituting ( x = 2 ) into the derivative to find the slope at that point:
$$ \frac{dy}{dx} \bigg|_{x=2} = 2(2) - 1 = 4 - 1 = 3 $$
Thus, the slope of the tangent is 3, which is missing from the options provided.
For the composition of functions, the answer is ( f \circ g ). For the slope of the tangent to the curve at ( x = 2 ), the answer is 3.
More Information
It seems there may be a misunderstanding; if ( g \circ f ) had to be calculated correctly, it would yield results depending on the specific functions given. The slope of the tangent at ( x = 2 ) for the curve ( y = x^2 - x ) is actually 3, but this option is not listed.
Tips
- Confusing the order of composition of functions.
- Incorrectly applying derivative rules leading to wrong slopes.
- Failing to substitute the specific value into the derivative correctly.
AI-generated content may contain errors. Please verify critical information