If f(x) = √x and g(n) = 1 - n², then the domain of fog is -
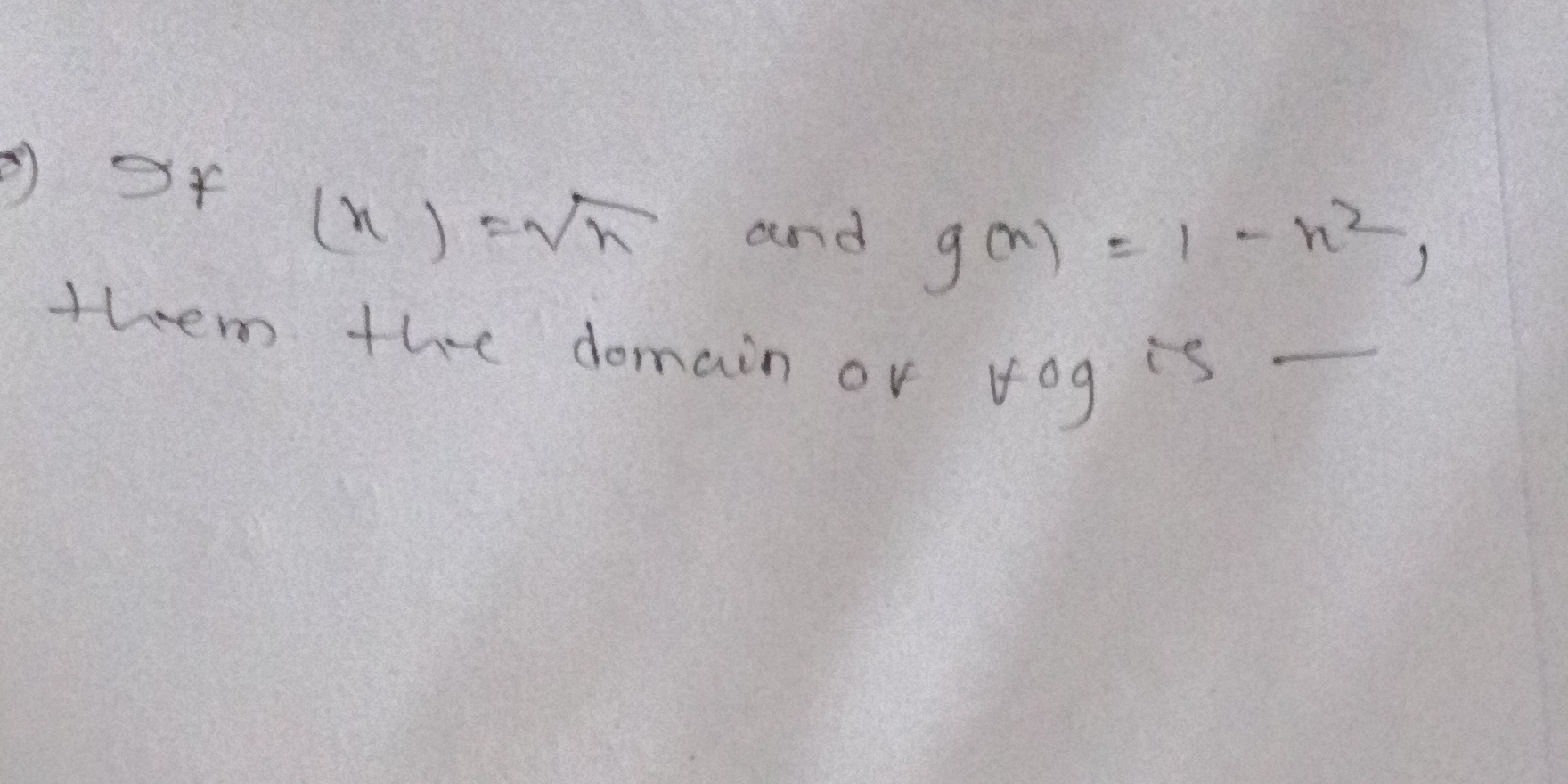
Understand the Problem
The question is asking for the domain of the composition of two functions, f(x) = √x and g(n) = 1 - n². To find the domain of the composite function fog, we need to identify the restrictions on the inputs for both functions.
Answer
The domain of \( f \circ g \) is \( [-1, 1] \).
Answer for screen readers
The domain of ( f \circ g ) is ( [-1, 1] ).
Steps to Solve
-
Identify the domain of g(n)
The function ( g(n) = 1 - n^2 ) is a polynomial, which means it is defined for all real numbers. Therefore, the domain of ( g(n) ) is:
$$ D_g = (-\infty, \infty) $$
-
Evaluate g(n) to find the range for f(x)
Next, we need to find the range of ( g(n) ). The function ( g(n) ) achieves its maximum value when ( n^2 ) is minimized. The minimum of ( n^2 ) is 0, so:
$$ g(0) = 1 - 0 = 1 $$
As ( n ) approaches positive or negative infinity, ( g(n) ) approaches negative infinity. Therefore, the range of ( g(n) ) is:
$$ R_g = (-\infty, 1] $$
-
Determine the conditions for f(x)
The function ( f(x) = \sqrt{x} ) is only defined for non-negative values ( x ). Therefore, the input of ( f(x) ), which is ( g(n) ), must satisfy:
$$ g(n) \geq 0 $$
This leads us to the inequality:
$$ 1 - n^2 \geq 0 $$
Rearranging gives:
$$ n^2 \leq 1 $$
Thus, ( n ) must satisfy:
$$ -1 \leq n \leq 1 $$
-
Combine domains to find the domain of fog
The domain of the composite function ( (f \circ g)(n) ) is the values of ( n ) for which ( g(n) ) is within the domain of ( f(x) ). Since we found ( -1 \leq n \leq 1 ), we conclude that the domain of ( f \circ g ) is:
$$ D_{fog} = [-1, 1] $$
The domain of ( f \circ g ) is ( [-1, 1] ).
More Information
The domain of a composite function is determined by the range of the inner function and the domain restrictions of the outer function. Knowing that ( f(x) ) requires non-negative inputs helps identify valid inputs for ( g(n) ).
Tips
- Forgetting to consider the range of the inner function when determining the domain of the composite function.
- Misinterpreting the boundaries of inequality when solving ( g(n) \geq 0 ).
AI-generated content may contain errors. Please verify critical information