If f(x) = 8 / sqrt(x + 2), find a formula for f^(-1)(y) and find the domain for f^(-1).
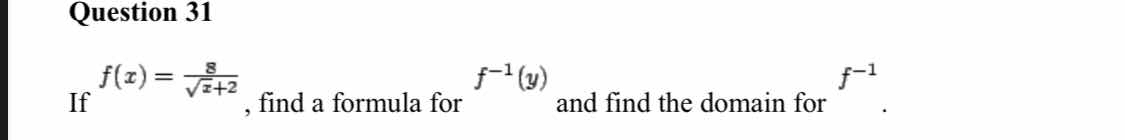
Understand the Problem
The question is asking to find the formula for the inverse function of a given function and also to determine the domain of that inverse function.
Answer
The formula for the inverse function is $f^{-1}(y) = \frac{64}{y^2} - 2$ and the domain is $(0, 4]$.
Answer for screen readers
The formula for the inverse function is: $$ f^{-1}(y) = \frac{64}{y^2} - 2 $$
The domain of the inverse function is: $$ (0, 4] $$
Steps to Solve
-
Rewrite the function Start with the given function: $$ f(x) = \frac{8}{\sqrt{x + 2}} $$
-
Set up for the inverse function To find the inverse, replace $f(x)$ with $y$: $$ y = \frac{8}{\sqrt{x + 2}} $$
-
Solve for x in terms of y Multiply both sides by $\sqrt{x + 2}$: $$ y \sqrt{x + 2} = 8 $$ Now divide by $y$ (assuming $y \neq 0$): $$ \sqrt{x + 2} = \frac{8}{y} $$
-
Square both sides Square both sides to eliminate the square root: $$ x + 2 = \left(\frac{8}{y}\right)^2 $$ This simplifies to: $$ x + 2 = \frac{64}{y^2} $$
-
Isolate x Subtract 2 from both sides: $$ x = \frac{64}{y^2} - 2 $$
-
Write the inverse function The inverse function is: $$ f^{-1}(y) = \frac{64}{y^2} - 2 $$
-
Determine the domain of the inverse function The domain of the inverse function corresponds to the range of the original function. Since the output of $f(x)$ must be positive, we find the minimum value:
- As $x \to -2$, $f(x) \to 4$ (since $f(-2) = 4$)
- As $x \to \infty$, $f(x) \to 0$
Thus, the range of $f(x)$ is $(0, 4]$.
- Write the domain of the inverse function Therefore, the domain of $f^{-1}(y)$ is: $$ 0 < y \leq 4 $$
The formula for the inverse function is: $$ f^{-1}(y) = \frac{64}{y^2} - 2 $$
The domain of the inverse function is: $$ (0, 4] $$
More Information
The inverse function allows us to revert from the output $y$ back to the input $x$. Understanding the relationship between a function and its inverse is fundamental in algebra and calculus.
Tips
- A common mistake is neglecting to properly square both sides when eliminating the square root, which can lead to incorrect solutions.
- Not checking the range of the original function to determine the domain of the inverse function.
AI-generated content may contain errors. Please verify critical information