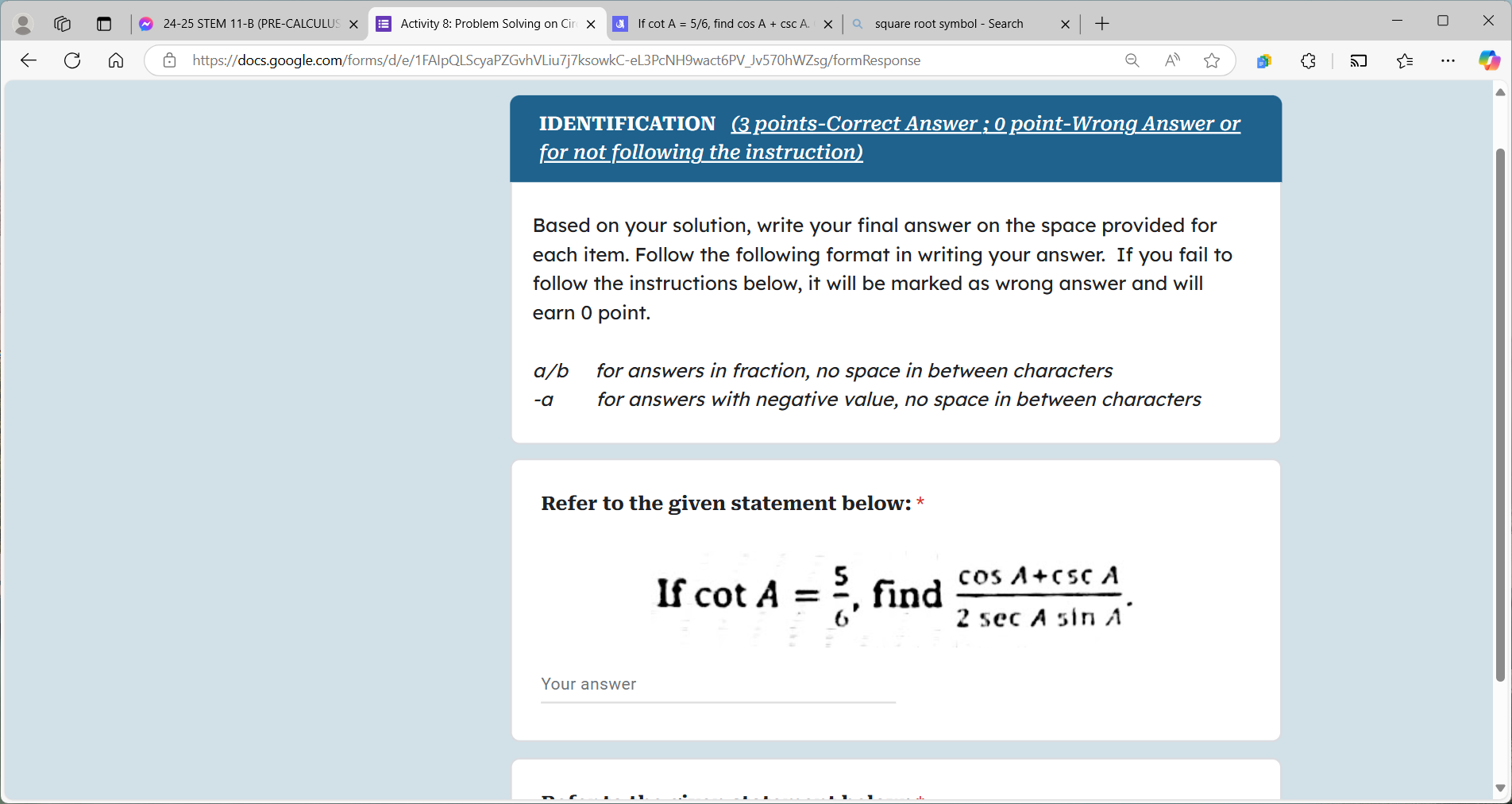
If cot A = 5/6, find cos A + csc A.

Steps to Solve

1. Identify cotangent relationship

Given that ( \cot A = \frac{5}{6} ), we can define opposite and adjacent sides. If the adjacent side is 5 and the opposite side is 6, then:

• Opposite = 6
• Adjacent = 5

2. Calculate hypotenuse using Pythagorean theorem

Using the relationship ( a^2 + b^2 = c^2 ), we find the hypotenuse ( c ): $$ c = \sqrt{5^2 + 6^2} = \sqrt{25 + 36} = \sqrt{61} $$

3. Find cosine and cosecant

Now, we can find ( \cos A ) and ( \csc A ) using:

• ( \cos A = \frac{\text{adjacent}}{\text{hypotenuse}} = \frac{5}{\sqrt{61}} )
• ( \csc A = \frac{\text{hypotenuse}}{\text{opposite}} = \frac{\sqrt{61}}{6} )

4. Substitute into expression

The expression we need to find is: $$ \frac{\cos A + \csc A}{2 \sec A \sin A} $$

5. Find ( \sec A ) and ( \sin A )

Calculating ( \sec A ): $$ \sec A = \frac{1}{\cos A} = \frac{\sqrt{61}}{5} $$ For ( \sin A ): $$ \sin A = \frac{\text{opposite}}{\text{hypotenuse}} = \frac{6}{\sqrt{61}} $$

6. Combine values into final expression

Plugging all values into the expression: $$ \frac{\frac{5}{\sqrt{61}} + \frac{\sqrt{61}}{6}}{2 \cdot \frac{\sqrt{61}}{5} \cdot \frac{6}{\sqrt{61}}} $$

7. Simplify the expression

First, simplify the denominator: $$ 2 \cdot \frac{\sqrt{61}}{5} \cdot \frac{6}{\sqrt{61}} = \frac{12}{5} $$

Next, simplify the numerator: $$ \frac{5}{\sqrt{61}} + \frac{\sqrt{61}}{6} = \frac{30 + \sqrt{61}^2}{6\sqrt{61}} = \frac{30 + 61}{6\sqrt{61}} = \frac{91}{6\sqrt{61}} $$

Therefore, the whole expression becomes: $$ \frac{\frac{91}{6\sqrt{61}}}{\frac{12}{5}} = \frac{91 \cdot 5}{6\sqrt{61} \cdot 12} $$

8. Final Calculation

This simplifies to: $$ \frac{455}{72\sqrt{61}} $$